| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 05.08.2009, 16:47 Titel: Physik der Musikinstrumente Verfasst am: 05.08.2009, 16:47 Titel: Physik der Musikinstrumente |
 |
|
Ein lehrreiches Thema ist die "Physik der Musikinstrumente". Thematisch gehört dieses Gebiet zur Mechanik, insbesondere zur Akustik. Der Wellenlehre kommt im Kontext eine grosse Bedeutung zu. Ohne Mathematik geht es nicht. Erst mit dem Aufkommen der Infinitesimalrechnung wurden die mit den Musikinstrumenten verbundenen Problematiken mathematisch beherrschbar.
Der erste ernstzunehmende Anstoss kam von Brook Taylor (1685-1731). Er erkannte, dass die Grundschwingung einer Seite durch eine Sinusfunktion beschrieben werden kann. D'Alembert, Euler und D. Bernoulli steuerten das ihrige zur Schwingungs- und Wellenlehre bei.
Dem Instrumentenbauer geläufig ist die alte Taylorsche Formel, die vom isochronen Pendel abgeleitet wurde:
f = (c/d)(D/L)√(P/N)
In heutiger praxisgängiger Form:
f = (1/2l)√(F/м)
м = Masse pro Längeneinheit := ρA
Damit lässt sich die Frequenz des Grundtons einer Saite berechnen. Der Saitenton ist um so tiefer, je länger die Saite, je kleiner die Zugspannung und je grösser die Saitenmasse ist. Tiefe Töne erfordern daher grosse Saitenmassen (was durch Umspinnen mit dünnem Kupfer- oder Silberdraht erreicht wird). Der Instrumentenbauer muss allerdings weitere Einflussgrössen berücksichtigen wie Zugfestigkeit, Dichte, Dehnung, Bruchdehnung, E-Modul und Härte einer Saite.
Die Bewegungsgleichung der eindimensionalen harmonischen Schwingung lautet:
x'' + ω²x = 0
Real muss die Dämpfung berücksichtigt werden, so dass gilt:
x'' + 2αx' + ω²x = 0
Modellbeispiele solcher Systeme sind:
- Masse-Feder-Pendel
- Helmholtz-Resonator
Als schwingende Systeme kommen instrumental in Betracht:
- Saiten: Geige, Gitarre, Klavier, Harfe
- Blätter: Oboe, Klarinette, Saxophon
- Membranen: Trommel, Pauke, Bongo
- Platten, Stäbe: Xylophon, Vibraphon, Triangel
- Schalen: Becken, Tam-Tam, Glocke, Gong
- Resonatoren: Orgelpfeife, Geigenkasten, Gitarrenkörper, Klavierkorpus
- Wellenleiter: Flöte, Trompete, Horn
Löst sich die Schwingung vom erzeugenden System, entsteht in der Luft eine longitudinale Raumwelle. Bei sphärisch-symmetrischer Quelle treten zudem Kugelwellen in Erscheinung.
Nach d'Alembert gilt allg. für eine Welle:
∂²y/∂t² = c²(∂²y/∂x²)
Ein weiterer Fortschritt setzte mit Fourier bzw. dessen Traktat "La Théorie Analytique de la Chaleur" ein, wo gezeigt wurde, dass eine Schwingung in verschiedene Teilschwingungen unterschiedlicher Stärke zerlegt werden kann. Entwickelt hatte Fourier sein Werkzeug für die Untersuchung von Temperaturschwankungen. Dies erwies sich wegweisend auch für die Akustik, so dass die von Mersenne und Sauveur phänomenologisch untersuchten Tonspektren nun auch mathematisch beschrieben werden konnten. Nicht lange danach erweiterten Ohm und Helmholtz das Wissen um die Obertöne. Insbesondere Ohm (1863) vermochte zu zeigen, dass das Gehör wie ein Fourieranalysator arbeitet. Helmholtz dagegen analysierte Klänge, indem er das Phänomen der Resonanz bemühte.
1) Beginnen wir bei Saiten und dünnen Stäben, wo nach dem Hooke'schen Gesetz eine Rückstellkraft zu verzeichnen ist:
F/S = E(∂w/∂x)
Je nach Befestigung des Stabes (ein- oder zweiseitig) sind viele Schwingungsmoden möglich. Reine Sinusschwingungen sind die Ausnahme, weil eine Saite auch Oberschwingungen erzeugt; doch das wusste Brook Taylor noch nicht. Bei der Gitarre sind es zur Hauptsache transversale Schwingungen der Saiten. Bei Stäben kommen auch Torsionsschwingungenn vor. Beim Klavier werden die Saiten durch eine Hammermechanik angestossen. Die Hämmer bestehen aus einem Hartholzkern mit Filzüberzug. Der charakteristische Klang entsteht durch das Zusammenwirken von Saiten, Steg und Resonanzboden. Nebst dem Anschlag ist auch das Abklingverhalten von Bedeutung; dabei überlagern sich horizontale und vertikale Saitenschwingungen. Bei der Geige ist der Einfluss des Bogendrucks auf die Saite zu beachten. Stets ist auch ein Einschwingvorgang vorhanden. Tonquellen mit Schallwand (Geige) sind auch bei niedrigen Frequenzen effizient. Zur mathematischen Behandlung wird das Fresnel-Kirchhoffsche Beugungsintegral bemüht.
2) Bei Membranen, Platten und Schalen müssen wir wegen der schwingenden Fläche die Wellengleichung zweidimensional entwickeln. Die ideale Membran ist als zweidimensionale Erweiterung der idealen Seite zu verstehen. Es ist zwischen Rechteck- und Kreismembran zu unterscheiden. Zur Beschreibung dünner Kreisplatten erweisen sich Besselfunktionen als nützlich. Die Eigenfrequenz einer runden Membran ist durch die zugehörige Nullstelle einer Besselfunktion n-ter Ordnung bestimmt.
Besselfunktionen 1. Gattung, n-ter Ordnung:
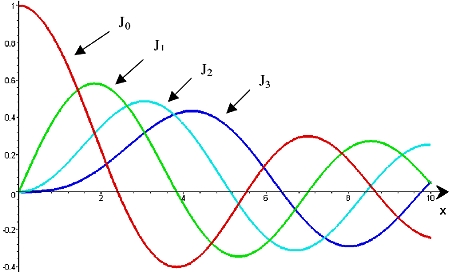
Anm.: Bessel-Funktionen (Zylinderfunktionen) spielen eine wichtige Rolle in der Physik. Man trifft sie u.a. bei der Untersuchung von Eigenschwingungen von zylindrischen Resonatoren, der Analyse des Frequenzspektrums von frequenzmodulierten Signalen (FM) und dem Sättigungsverhalten von Klystrons (Radartechnik, Beschleunigerphysik).
Zahlreich ist auch das Modenspektrum quadratischer Platten wie die Chladnischen Klangfiguren belegen:

Anm.: Auf die Platte gestreuter Sand wandert zu den Knotenpunkten der Wellenfläche, so dass sich die zum jeweiligen Klangbild charakteristische Figur einstellt.
In dünnen Platten manifestieren sich Longitudinal- und Transversalwellen ohne signifikante Abstrahlung. Hingegen treten stark dispersive Biegewellen mit signifikanter Abstrahlung auf. Die Frequenz der Normalmoden hängt von den Randbedingungen ab. Nebst der Erzeugung von Harmonischen sind auch Subharmonische zu beobachten. Selbst chaotisches Verhalten kommt vor.
3) Als Wellenleiter - insbesondere bei Blasinstrumenten - dienen lange Zylinderrohre und Hörner; zudem ist zwischen konischen und hyperbolischen Hörnern zu unterscheiden. Exponential- und Besselhorn seien erwähnt. Die ideale Bohrung für die Klarinette ist eine über die gesamte Länge verlaufende zylindrische Bohrung. Wegen ihrer drei Register unterscheidet sich die Klangfarbe über mehrere Oktaven beachtlich (in der tiefen Lage sind die ungeradzahligen Obertöne lauter, in der hohen Lage die geradzahligen). Oboe, Saxophon und Fagott besitzen hingegen konische Bohrungen.
Stehende Wellen entstehen im Rohr als Überlagerung zweier gegenläufiger Wellen. Die rücklaufende Welle entsteht durch Reflexion. Bedingung dafür ist ein Übergang mit unterschiedlicher Impedanz. In Pfeifen haben wir es immer mit stehenden Wellen zu tun.
Für offene Pfeifen gilt: f = c/(2l)
Für geschlossene dagegen: f = c/(4l)
Bei der Trompete wird die Länge der schwingenden Luftsäule über Ventile gesteuert. Massgebend für den Klang ist auch die Mensur. Mundstück, Lippentechnik und allenfalls ein Dämpfer beeinflussen die Tonqualität.
Diese Kurzeinführung in die "Physik der Musikinstrumente" zeigt bereits deutlich, dass ohne höhere Mathematik kein tieferes Verständnis der zugrunde liegenden Phänomene möglich ist. Die Mathematik erweist sich in dieser Sache als treue Schwester der Physik. Hinzu kommt das einschlägige Experiment, wie es dem Studenten bspw. aus dem Physikalischen Praktikum bekannt ist.
Soviel für heute.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 06.08.2009, 17:01 Titel: Verfasst am: 06.08.2009, 17:01 Titel: |
 |
|
Geräusch, Ton, Klang und Harmonie
1) Ein reiner Ton ist eine Sinusschwingung. Der für ein bestimmtes Instrument charakteristische Klang besteht aus einer Superposition mehrerer sinusförmiger Schwingungen zu einer nicht sinusförmigen. Der Grundton bestimmt die Tonhöhe, die Obertöne die Klangfarbe.
Ein Geräusch, z.B. das Rascheln von Papier, ist ein stochastisches Schwingungsphänomen, ein Gemisch sehr vieler Frequenzen ungefähr gleicher Intensität.
Ein Knall, z.B. beim Platzen eines Luftballons, ist ein kurzzeitiger und starker Schalleindruck. Für den Experimentalphysiker ist es ein Diracstoss.
2) Im Abendland existieren grundsätzlich zwei Tonleitern.
2.1) Die diatonische Tonleiter umfasst folgende Intervalle:
Prime, Sekunde, Terz, Quarte, Quinte, Sexte, Septime und Oktave. Letztere bedeutet eine Frequenzverdopplung. Je zwei benachbarte Töne (Intervall) stehen in einem bestimmten Frequenzverhältnis, bezogen auf den Grundton:
c = 1; d = 9/8; e = 5/4; f = 4/3; g = 3/2; a = 5/3; h = 15/8; c' = 2/1
Einer hat einmal gesagt: Musik ist Mathematik. In obigem Sinne stimmt dies auch.
2.2) Die chromatische Tonleiter besitzt zusätzliche Halbtöne, damit auch auf anderen Grundtönen aufgebaut werden kann, nämlich:
cis (des), dis (es), fis (ges), gis (as), ais (b)
3) Für Instrumente mit fester Stimmung (Klavier) ist die chromatische Tonleiter mit ihrer reinen Stimmung nicht brauchbar. Anstatt dessen wird die gleichmässig temperierte Tonleiter verwendet. Jedes der aufeinander folgenden 12 Halbtonintervalle besitzt hier das gleiche Frequenzverhältnis von sqrt2^(1/12) = 1.059463...
Als Kammerton gilt das eingestrichene a' (f = 440 Hz). Mit diesem "wohltemperierten Klavier" erst ist es möglich, auf jedem der 12 Töne einer Oktave sowohl eine Dur- wie auch eine Molltonleiter aufzubauen.
4) Letztlich erhalten wir den Quintenzirkel, an welchem sich Klavier, Solostimme und Orchester orientieren.
Quintenzirkel (mit Dur- und Moll-Tonarten):

Anm.: Jede der zwölf Tonarten ist durch eine Quinte von der benachbarten entfernt. Diese Verwendung der Tonarten sowie die dazu notwendige temperierte Stimmung sind schöpferische Leistungen der abendländischen Kultur, die es in anderen Kulturen in dieser Form nicht gibt. Ohne temperierte Stimmung - bei Verwendung reiner Quinten - entstünde eine Quintenspirale. Erst die wohltemperierte Stimmung ermöglicht die "enharmonische Verwechslung" und somit einen geschlossenen Zirkel.
Ein Klarinettist, der auf seinem Instrument in Cis-Dur (Des) spielt, benötigt wegen der vielen zu betätigenden Klappen einige Fingerfertigkeit. Benutzt er bspw. eine in B gestimmte Klarinette, muss ihn das Klavier auf H-Dur begleiten. Benutzt er eine A-Klarinette, spielt der Pianist in B-Dur. Oft verwendet der gewiefte Jazzklarinettist deshalb zwei unterschiedlich gestimmte Klarinetten, um so bei schwierigen Stücken die für ihn günstigste Stimmlage greifen zu können. Jedenfalls habe ich diese Praxis bereits als Junge übernommen, wenn der Alte seiner Klavierhandorgel nie gehörte Klänge entlockte und ich ihn dazu auf der Klarinette begleiten durfte... Als wir 'The Sheik of Araby' oder 'Honeysuckle Rose' und andere griffige Stücke spielten. Oder auch 'Friedas Traum' und 'Auf Wiedersehn' mit beschwingtem Foxtrott-Einschlag. Harmonisch empfundene Tonartenwechsel erfolgen oft im Gegenuhrzeigersinn; aber auch das Umgekehrte ist natürlich möglich. So wechselten wir bspw. von F-Dur nach B-Dur und danach erneut zurück nach F-Dur. Im alten Jazz gibt es viele Varianten; deshalb höre ich zwischendurch gerne ausgesprochenen Klarinettenvirtuosen wie Johnny Dodds (1892-1940), Jimmie Noone (1895-1944), George Lewis (1900-1968), Barney Bigard (1906-1980), Benny Goodman (1909-1986), Ernst Höllerhagen (1912-1956) u.a. Oldman's zu, während ihre unvergessliche Musik aus alten Schellackplatten erklingt.
5) Von der Stimmlage und Empfindung her gibt es zwei grundsätzliche Tonspektren. Bei einer Dur-Tonart liegen die Halbtonintervalle zwischen dem 3. und 4. bzw. 7. und 8. Ton, bei einer Moll-Tonart zwischen dem 2. und 3. bzw. 5. und 6. Ton. Moll erzeugt eine eher gedrückte, zuweilen sogar düstere Stimmung (lausche Schuberts Unvollendeter - eine Sinfonie in h-Moll). Zigeuner spielen virtuos in ihrem eigenen Moll. Am Schönsten für mich sind die gemischten Chöre aus der freikirchlichen Bewegung. In Deutschland gab's früher auch solche. Dann kommen mir aus tiefster Seele dicke Tränen, weil ich weiss, was Er am Kreuze für uns tat. Der Klang, die Harmonie und die Worte bewegen mich - ansonsten ein Mann wie eine Eiche - jeweils aufs Heftigste. Wenn einst selbst ich Geringer im höhern Chor steh', bekleidet mit weissem Gewand und Palmblatt in der einen Hand - wird dies nicht eine unaussprechliche Freude sein? Doch, gewiss, Überwinder will ich sein.
6) Nichts ist mir mehr verhasst, als dissonante Intervalle. Wohlklingende, d.h. konsonante Intervalle sind z.B. Terz und Quinte. Das gleichzeitige Erklingen einzelner Töne, die harmonisch empfunden werden, wird als Akkord bezeichnet. Gewisse Akkorde, wie z.B. ein C-Dur-Akkord, wirken hell und freundlich. Moll-Akkorde sind dagegen eher trübe und traurig. Andere, wie der Septimenakkord, besitzen eine intensive Klangfarbe. Der verminderte Septimenakkord birgt eine Spannung in sich, die der baldigen Auflösung harrt. Dramatisch wirken Nonenakkorde auf mein Gemüte ein. Harmonielehre ist gewiss eine kunstvolle Disziplin; doch niemand weiss, weshalb wir so empfinden.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 06.08.2009, 21:08 Titel: Verfasst am: 06.08.2009, 21:08 Titel: |
 |
|
| zeitgenosse hat Folgendes geschrieben: |
3) Für Instrumente mit fester Stimmung (Klavier) ist die chromatische Tonleiter mit ihrer reinen Stimmung nicht brauchbar. Anstatt dessen wird die gleichmässig temperierte Tonleiter verwendet. Jedes der aufeinander folgenden 12 Halbtonintervalle besitzt hier das gleiche Frequenzverhältnis von sqrt2^(1/12) = 1.059463...
|
das weiß übrigens auch jeder Gitarrenbauer. Die Position der Bünde der Gitarre wird genau über \(2^{1/12}\) berechnet. Für den ersten Bund wird also die Mensur (die Länge zwischen Bundsteg unten und Bundsteg oben) durch \(2^{1/12}\) geteilt. Das Ergebnis gibt den Abstand vom unteren Bundsteg (wo auch die Tonabnehmer sitzen) zum ersten Bund. Pro Bund kommt dann eine weitere Division durch \(2^{1/12}\) hinzu, bis man beim 12ten Bund genau eine Division durch 2 erhält und damit die Oktave bei den Frequenzen.
Mit diesem Wissen, etwas handwerklichem Geschick, dem richtigen Holz, etwas Mechanik für die Saiten und mindestens einem Tonabnehmer kann man sich dann zumindest theoretisch eine Gitarre selberbauen. Jeder der sich mit Gitarrenbau einmal näher beschäftigt hat, weiß allerdings, dass der Bau einer hochwertigen (E-)Gitarre eine ziemlich diffizile Angelegenheit ist.
MfG |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 06.08.2009, 21:30 Titel: Verfasst am: 06.08.2009, 21:30 Titel: |
 |
|
| Barney hat Folgendes geschrieben: | | Mit diesem Wissen, etwas handwerklichem Geschick, dem richtigen Holz, etwas Mechanik für die Saiten und mindestens einem Tonabnehmer kann man sich dann zumindest theoretisch eine Gitarre selberbauen. |
Leider verstehe ich von akustischen Gitarren zuwenig, um ernsthaft mitreden zu können. Viele Musiker wissen es auch nicht besser; dafür spielen sie mit Bravour auf den Saiten.
Anders sieht es beim Gitarrenverstärker aus. Hier könnte ich mir gut vorstellen, einen transportablen selbst zu bauen. Selbstverständlich einen solchen mit zwei glühenden Endpentoden.
P.P.P. (Gegenparallel) Endverstärker:

In jedem Fall ist es ein solides Handwerk, gepaart mit Erfahrungswissen und gründlichen Materialkenntnissen.
Wenn man zudem versteht, wie das jahrhundertealte Problem der schwingenden Saite mittels einer Differentialgleichung gelöst wurde, darf man mit sich zufrieden sein.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 07.08.2009, 03:40 Titel: Verfasst am: 07.08.2009, 03:40 Titel: |
 |
|
| Barney hat Folgendes geschrieben: | | Die Position der Bünde der Gitarre wird genau über \(2^{1/12}\) berechnet. |
Für den Hinweis mit dem Zaunpfahl nachträglichen Dank. Wollte die 12. Wurzel aus 2 durch Potenzschreibweise, also \(2^{1/12}\) ausdrücken, so dass mein leichtsinnig hingeschriebenes "sqrt" natürlich überflüssig wird.
Vielleicht erbarmt sich Karl meiner und tilgt den Lapsus (bin in solchen Dingen nämlich äusserst pedantisch veranlagt).
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 07.08.2009, 08:37 Titel: Verfasst am: 07.08.2009, 08:37 Titel: |
 |
|
Hallo zeitgenosse,
manchmal ist es eben auch gut den Dingen ihren Lauf zu lassen. Der Insider weiß, was mit sqrt2^12 gemeint ist und für mich war es ein schöner Anlaß etwas über Gitarrenbünde zu schreiben.
Ich habe mir übrigens tatsächlich mal eine Gitarre selber gebaut und dabei die Bünde selbst berechnet. Der Tonabnehmer wurde mit Kupferlitze gewickelt und mit Gießharz fixiert. Das hat alles ziemlich viel Spaß gemacht und der Klang der Gitarre war auch ziemlich OK. Leider war der Hals etwas verzogen, so daß der Abstand der Saiten zu den Bünden so groß war, dass man langfristig keinen allzu großen Spaß mit dem Instrument hatte und nach einiger Zeit alles dem Sperrmüll zugeführt werden musste. Trotzdem war der Selbstbau eine interessante Erfahrung.
Besten Dank auch für den Schaltplan. Röhrenverstärker sind der Traum eines jeden E-Gitarre-Spielers und da ist es schön, wenn das Wissen darum gepflegt wird  ... ...
MfG |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 07.08.2009, 08:40 Titel: Verfasst am: 07.08.2009, 08:40 Titel: |
 |
|
Nach dem kurzen Abstecher in die Musiktheorie und Harmonielehre nun zum menschlichen Gehör. Dieses beziehe ich im erweiterten Kontext mitein in die "Physik der Musikinstrumente"; denn was nützt das schönste Instrumentenspiel, wenn es niemand hört?
A) Ein Versuch, die Physiologie des Ohres zu verstehen
1) Das Gehör des Menschen ist ein Kunstgebilde sondergleichen und zudem ein Organ von erstaunlicher Leistungsfähigkeit bezüglich der Wandlung mechanischer Schwingungen in elektrische Signale. Es nimmt Schallintensitäten von von 1e-12 bis 2 W/qm in einem Frequenzbereich von etwa 16 Hz bis 20 kHz wahr (sofern es gesund und nicht altersbedingt abgenutzt ist). Die Auflösung ist beachtlich. Das menschliche Ohr ist im Stande, Frequenzunterschiede von nur 3 Hz zu detektieren. Der kleinste noch hörbare Schallwechseldruck von 2e-5 Pa erzeugt eine Elongation des Trommelfells von gerade nur 1e-10 m (das entspricht dem Durchmesser eines Atoms).
Hörflächen-Diagramm (zwischen Reizschwelle und Schmerzgrenze):

Quelle: Kuchling, Taschenbuch der Physik
Erstaunlich ist auch die Fähigkeit der Klang- und Spektralanalyse (wobei die Weiterverarbeitung der Signalspektren im Gehirn stattfindet) - wie an den nachfolgenden Lautstärke-Zeit-Diagrammen ersichtlich ist:

Quelle: Bergmann/Schaefer, Experimentalphysik Bd. 1
a) Mendelssohns Violinkonzert
b) Stimmen eines Orchesters (Kakophonie)
c) Geräusche des Publikums während der Pause
Der Hör-Gehirn-Apparat vermag diese völlig verschiedenen Informationsgehalte tadellos zu unterscheiden, was selbst für einen entsprechend propgrammierten Spektrumanalyzer ein schwieriges Unterfangen bliebe.
Pohl vermerkt denn auch folgerichtig zum Spektralapparat des menschlichen Innenohres:
| Zitat: | | Was er leistet, ist physikalisch nur als eine "Vorzerlegung" zu bezeichnen. Das tatsächlich vorhandene grosse Auflösungsvermögen ist physikalisch nicht zu verstehen. Wie beim Auge stossen wir auch beim Ohr auf eine entscheidende Mitwirkung zentraler, also im Gehirn ablaufender Vorgänge. Sie entziehen sich einstweilen noch unserem Verständnis... |
Inzwischen wissen wir zwar erheblich mehr darüber, trotzdem ist es noch immer erstaunlich!
2) Organisch ist das Gehör unterteilt in Aussenohr, Mittelohr und Innenohr.
2.1) Durch den aussen befindlichen Gehörgang gelangt der Schall zum Trommelfell, einer Membran, welche auf die im Mittelohr vorhandenen Gehörknöchelchen einwirkt. Diese bestehen aus drei Gliedern - dem Hammer, der unmittelbar vom Trommelfell zum Schwingen angestossen wird und diese Oszillationen über Amboss und Steigbügel auf eine kleinere Membran - das ovale Fenster der Hörschnecke - überträgt. Rein mechanisch gesehen bereits ein subtiles Wunderwerk. Auch über die Schädelknochen erfolgt Schallausbreitung (setze eine schwingende Stimmgabel an die Stirn und du hörst den Ton intensiver).
2.2) Der eigentliche Schallwandler - die Cochlea - befindet sich eingebettet im Felsenbein des Innenohrs, ummantelt von einem äusserst harten Knochenmaterial. Dieses an ein Schneckengehäuse erinnernde Kunstwerk ist mit dem aus drei Bogengängen aufgebauten Gleichgewichtsorgan zu einer organischen Einheit verbunden und mit Flüssigkeit (Lymphe) gefüllt. Nebst dem ovalen Fenster - an welches der Steigbügel ansetzt - besitzt die Hörschnecke ein zweites rundes Fenster, das dem Druckausgleich dient.
3) Betrachten wir nun das Innenohr (Auris interna) im Detail - insgesamt ein hochkomplexes Organum; dessen Erfinder muss ein genialer Konstrukteur gewesen sein.
Ausguss eines menschlichen Labyrinths:
http://upload.wikimedia.org/wikipedia/commons/6/63/Ear_labyrinth.jpg
Unterteilt in zwei Kammern oder Gänge wird die Hörschnecke (Cochlea) entlang ihrer gewendelten Längsrichtung durch die Basilarmembran (Membrana basilaris), die - in der Breite anwachsend - ins Schneckenloch (Helicotrema) einmündet. Die mit Perilymphe angefüllten Kammern werden als 'Scala tympani' (Paukentreppe) und 'Scala vestibuli' (Vorhoftreppe) bezeichnet und sind miteinander an der Schneckenspitze (Apex) über das Schneckenloch verbunden. Eine dritte mit (kaliumreicher) Endolymphe gefüllte Kammer, die 'Scala media' - auch 'Ductus cochlearis' genannt -, ist durch die Reissner-Membran von der 'Scala vestibuli' und durch die Basilarmembran von der 'Scala tympani' getrennt und liegt zwischen den beiden anderen Gängen in der Hörschnecke.
Ductus cochlearis (Schneckengang) oder auch Scala media (mittlere Treppe):
http://upload.wikimedia.org/wikipedia/commons/d/d2/Ductus_cochlearis_schema.jpg
| Zitat: | | Der Ductus cochlearis beinhaltet das Corti-Organ mit den Haarzellen und der Membrana tectoria, einer dünnen Membran, die über dem Corti-Organ liegt und außerhalb der äußeren Haarzellen frei endet. |
Cochlea (schematisch):
http://upload.wikimedia.org/wikipedia/commons/5/58/Cochlea-crosssection-de.png
Zusammenfassend:
Die Basis der Hörschnecke grenzt an das Mittelohr mit den Gehörknöchelchen. Die Fußplatte des Steigbügels ist in das ovale Fenster (Fenestra vestibuli oder Fenestra ovalis) beweglich eingepasst. Hinter dem ovalen Fenster liegt die 'Scala vestibuli'. Diese ist an der Spitze der Schnecke über das Schneckenloch mit der 'Scala tympani' verbunden. Letztere grenzt an der Basis an das runde Fenster (Fenestra cochleae). Über das runde Fenster kann der durch die Oszillationen ausgeübte Druck ausgeglichen werden. Wird nun das ovale Fenster durch den Steigbügel in Schwingungen vesrsetzt, läuft eine Wanderwelle durch die 'Scala vestibuli' in Richtung Schneckenspitze; dies führt zur Auslenkung der Basilarmembran, wodurch der ausgeübte Flüssigkeitsdruck auf die 'Scala tympani' und schliesslich über die Tektorialmembran durch Scherung auf die äusseren Haarzellen des Cortischen Organs (Organon spirale) übertragen wird. Das Cortische Organ ist mit insgesamt vier Reihen feiner Haarzellen besetzt und sitzt auf der Basilarmembran. Die äusseren drei Reihen dienen der Verstärkung der mechanischen Schwingungen innerhalb der Cochlea (Verstärkungsfaktor V= 1000). Die innere Reihe bewirkt die Umwandlung der Oszillationen in Nervenimpulse (sog. mechano-elektrische Transduktion), welche über den Hörnerv als neuronale Impulsmuster ins Gehirn gelangen.
Fortsetzung folgt...
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 08.08.2009, 12:06 Titel: Verfasst am: 08.08.2009, 12:06 Titel: |
 |
|
B) Zur "Physik des Ohrs"
1) Es lässt sich im Modellversuch belegen, dass das Amplitudenmaximum der sich entlang der Basilarmembran ausbreitenden Wellengruppen eindeutig von der Frequenz abhängig ist. Jede Schallfrequenz besitzt ihren Ort auf der Basilarmembran. Diese wirkt also in gewisser Weise wie ein mit einem Zungenfrequenzmeter vergleichbarer Spektralapparat (was bereits von Ohm vermutet wurde) - nur eben wesentlich umfassender in Aufbau und Perfomance.
Lineares Modell der Hörschnecke (ähnliche Modelle sind von Diestel und Dorendorf bekannt):

Quelle: Pohl, Einführung in die Physik, Bd. 1
Zwei Kammern rechteckigen Querschnitts sind mit Glaswänden abgeschlossen und mittig durch eine hochelastische Membran von keilförmigem Zuschnitt getrennt. Als Membran dient die Grenzfläche zweier Flüssigkeiten verschiedener Dichte und Oberflächenspannung (oben Benzol, unten Wasser mit einem Additiv). Der Steigbügel wirkt - über einen Exzenter angetrieben - auf das ovale Fenster ein. Dieses wird somit zum Ausgangsort einer Wellengruppe, die entlang der Basilarmembran in Richtung des Schneckenlochs wandert. Auch bei sinusförmiger Erregung bilden sich charakteristische Wellengruppen aus, deren Gruppengeschwindigkeit nach Erreichen der maximalen Amplitude rasch abfällt.
2) Unterschiede zum Modell:
Real besteht die Schnecke aus einer knöchernen Hülle, die drei übereinander liegende spiralig aufgewickelte konische Röhren (Gänge) enthält. Basilarmembran und Schneckenkanal wirken zusammen als mechanisches Resonatorsystem. Weil die Breite der keilförmgen Basilarmembran (anfangs schmal und dick) - sowie auch der Durchmesser des Schneckenkanals - vom ovalen Fenster zum Helicotrema hin zunehmen, ändern sich stetig die örtlichen mechanischen Eigenschaften des Systems entlang des Schneckenganges. Dies führt dazu, dass die Basilarmembran für unterschiedliche Frequenzen an unterschiedlichen Stellen ihr Erregungsmaximum (Resonanz) besitzt. Dazu ist die Basilarmembran in etwa 24 gleich lange Abschnitte (Frequenzgruppen) unterteilt . Die Breite einer Frequenzgruppe beträgt ca. 100 Hz bei Frequenzen bis 500 Hz und eine kleine Terz oberhalb von 500 Hz. Wegen der hohen Steife der Basilarmembran erzeugen hohe Frequenzen in der Nähe des ovalen Fensters ein Amplitudenmaximum. In Richtung Helicotrema, wo die Membran breiter und dünner wird, schwingt sie dagegen mit niedrigerer Frequenz (bei größerer Amplitude). Für diese Erkenntnisse bekam Békésy 1961 den Nobelpreis.
Fazit:
Die mechano-elektrische Schallwandlung im Gehör und die anschliessende Informationsverarbeitung von Signalmustern im Gehirn zählen zu den anspruchsvollsten Vorgängen in der Natur, die mir immer wieder allergrössten Respekt vor dem unsichtbaren "Watchmaker" abverlangen. Selbst heute ist noch vieles nicht restlos geklärt. Der nachfolgende Link zeigt nochmals die umfassende Problematik:
http://de.wikipedia.org/wiki/Universalien_der_Musikwahrnehmung
3) Zur Bewertung empfundener Tonhöhen wurden zwei Skalen entwickelt. Mitels psychoakustischer Versuche kann so die Tonheitsskala bestimmt werden.
3.1) Mel-Skala
Das Mel (von "melody") ist die Masseinheit für die psychoakustische Größe "Tonheit Z" und beschreibt die die Tonhöhenwahrnehmung. Die Mel-Skala wurde 1937 von Stevens, Volkman und Newmann vorgeschlagen.
Es gibt zwei Definitionen der Mel-Skala, die sich jeweils im Referenzwert unterscheiden:
a) Nach Stanley Smith Stevens ist der Referenzton mit f = 1000 Hz die Bezugsbasis der Mel-Skala := Z = 1000 mel
b) Nach Eberhard Zwicker ist der muskalische Ton C die Bezugsbasis der Mel-Skala := Z = 131 mel
In beiden Definitionen gilt: Ein Ton, der doppelt so hoch wahrgenommen wird, erhält den doppelten Tonheitswert; ein Ton, der halb so hoch wahrgenommen wird, den halben Tonheitswert.
3.2) Bark-Skala
Diese nach Heinrich Barkhausen benannte psychoakustische Skala für die wahrgenommene Tonhöhe ist definiert von 0,2 bis 25 Bark. Eine Verdoppelung des Bark-Wertes bedeutet, dass der entsprechende Ton als doppelt so hoch empfunden wird.
Es gilt: 1 bark = 100 mel
Normiert werden Bark- als auch modifizierte Mel-Skala auf den musikalischen Ton C (131 Hz).
Einheitenkonversion:
http://www.ling.su.se/staff/hartmut/umrechnung.htm
Fortsetzung folgt...
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 08.08.2009, 12:15 Titel: Verfasst am: 08.08.2009, 12:15 Titel: |
 |
|
Abschliessend die gebräuchlichsten im Kontext vorkommenden physikalischen Grössen, die für messtechnische Zwecke nützlich sind.
Schallschnelle in [m/s]
Darunter versteht man die Schwinggeschwindigkeit der Teilchen eines Mediums:
v = (ωy_max)cosωt
y_max = Spitzenwert (Amplitude)
ω = Kreisfrequenz
ωt = Phasenwinkel
Daraus folgt für die max. Schnelle:
v_max = ωy_max
Meist wird die Schallschnelle nicht gemessen, sondern aus dem Schalldruck errechnet.
Schalldruck in [N/qm]
Darunter versteht man die in einer Schallwelle vorkommenden periodischen Druckabweichungen (Unter-, Über- und Wechseldruck):
p = (ωρcy_max)cos2π [(t/T) - (x/λ)]
ρ = Dichte des Mediums
c = mediumspezifische Schallgeschwindigkeit
T = Schwingungsdauer (Periode)
λ = Wellenlänge
x = Abstand vom Wellenzentrum
Daraus folgt für die Druckamplitude:
p_max = ρcωy_max = ρcv_max
Schallintensität (Schallstärke) in [W/qm]
Darunter versteht man das Verhältnis der auf eine Fläche treffenden Schalleistung zur Grösse dieser Fläche:
J = P/A
Schallpegel in [dB]
Darunter versteht man ein Vergleichsmass zweier Schallintensitäten oder Schalldrücke:
a) L_J = 10lg(J/J_o)dB
J = zu bestimmende Schallintensität
J_o = Bezugsschallintensität [1 pW/qm]
b) L_p = 20lg(p/p_o)dB
p = zu bestimmender Schalldruck
p_o = Bezugsschalldruck [20 μPa]
Relativer Schallpegel in [dB]
Darunter versteht man die Differenz zweier absoluter Schallpegel L1 - L2:
a) ΔL_J = 10lg(J1/J2)db
b) ΔL_p =20lg(p1/p2)dB
Eine bekannte Anwendung ist das in der Bautechnik verwendete Schalldämm-Mass:
R = 10lg(J1/J2)dB = 20lg(p1/p2)dB
Lautstärkepegel in Phon [phon]
Darunter versteht man eine physiologisch bedingte Grösse (Lautstärke, die subjektiv als Schallstärke empfunden wird):
L_N = 20lg(p/p_o)phon
p = Schalldruck eines gleich laut empfundenen 1000 Hz Tones
p_o = Bezugsschalldruck [20 μPa]
Pegeldiagramm:

Quelle: Kuchling, Taschenbuch der Physik
Beachte: Für einen Ton mit f = 1000 Hz stimmen Schalldruckpegel L und Lautstärkepegel L_N überein. Die Schallempfindung wächst gemäss dem Weber-Fechnerschen Gesetz mit dem Logarithmus der Schallintensität.
Zur Festigung (natürlich nur für willige Teilnehmer) ein paar leichtere Übungen:
α) In einer kugelförmigen Lautsprecherbox - wie soll's auch anders sein - breitet sich der Schall kugelsymmetrisch aus. In welcher Beziehung steht die Schallintensität zum Kugelradius der Box?
β) Bei einer Gehörprüfung vernimmt der Proband ein in 3 m Entfernung leise gesprochenes Wort noch gut, in 8 m Entfernung jedoch nicht mehr. Wie gross ist demzufolge der Schalldruckpegel in 3 m Abstand?
γ) Ein Träger aus Chromnickelstahl (ρ = 8 kg/dm³) mit den Abmessungen l = 4 m und A = 0.01 qm wird mit einem Gewicht von 1 t in Achsrichtung belastet. Mit einem Ultraschallsignal (axiale Laufzeit = 0.6 ms) soll die Längenänderung (Deformation) des Trägers ermittelt werden. Wie gross ist diese?
Damit ist dem sog. "Sommerloch" im Sinne nützlichen Überbrückungs-Entertainments Genüge getan und ich kann mich zwischendurch wieder andern Aktivitäten widmen.
Ach, was ich noch zu erwähnen vergass:
Es gibt ein hübsches Buch von Klaus Winkler (vermutlich ist es inzwischen vergriffen):
Die Physik der Musikinstrumente (Spektrum Akad. Vlg)
Wer sich dafür interessiert, müsste auf Amazon o.ä. fündig werden.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 10.08.2009, 00:43 Titel: Verfasst am: 10.08.2009, 00:43 Titel: |
 |
|
Auflösung (Vorbeitrag) der leichten Fingerübungen:
α) Die Schallintensität ist repräsentant für die Energiedichte (Schallleistung durch Kugeloberfläche --> A = 4πr²).
Daraus folgt: Schallintensität: J ~ 1/r²
β) J1/J2 = r2²/r1² ; J2 = 9J1/64
L1 - L0 = 10lg(64/9) = 8.5 dB
γ) Nach Hooke ist σ = Eε
Aus Dehnung ε = Δl/l und Zugspannung σ = F/A = mg/A folgt die Deformation:
Δl = εl = lmg/(EA)
In festen Körpern gilt für die Ausbreitungsgeschwindigkeit von Schallwelllen die Beziehung:
c = sqrt(E/ρ) = l/t
Daraus folgt: E = ρl²/t²
so dass: Δl = mgt²/(ρlA) = 1.104e-5m
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 12.08.2009, 15:03 Titel: Verfasst am: 12.08.2009, 15:03 Titel: |
 |
|
Nachtrag I
Zum Problem der schwingenden Saite (für gestandene Physiker ein Klacks, für sonstige Leser womöglich eine nützliche Wissenserweiterung).
Historischer Exkurs:
Bereits die Pythagoräer beschäftigten sich mit der schwingenden Saite des Monochords und stellten einen Zusammenhang zwischen der Länge und der Tonhöhe fest.
Gaudentius bemerkt dazu:
| Zitat: | | Pythagoras spannte eine Saite über einen Kanon (Massstab) und teilte ihn in zwölf Töne. Dann liess er zunächst die ganze Saite ertönen, darauf die Hälfte, d.h. sechs Teile, und er fand, dass die ganze Saite zu ihrer Hälfte konsonant sei, und zwar nach dem Zusammenklang der Oktave. Nachdem er darauf die ganze Saite, dann Dreiviertel von ihr hatte erklingen lassen, erkannte er die Konsonanz der Quarte und analog für die Quinte. |
Ungeachtet aller geistigen Bemühungen der Antike wurde das Kernproblem erst im ausgehenden 18. Jahrhundert befriedigend gelöst, als man bereits im Besitze des "Calculus" war und allmählich auch mit partiellen Differentialgleichungen umzugehen verstand. Vorauslaufend erfolgten die mit einem experimentellen Ansatz behafteten Arbeiten von Mersenne (Harmonie Universelle, 1636) und Galilei (Discorsi, 1638), die aber nicht über die elementarsten Aspekte hinausgingen.
Das Problem ist nämlich folgendes:
Eine beidseitig fest eingespannte elastische Saite schwingt nebst ihrer Grundmode (L = λ/2) auch auf ganzzahligen Vielfachen. Diese Moden werden als Harmonische n-ter Ordnung bezeichnet. Darüber wussten die Alten einfach zuwenig. Eine weitere Schwierigkeit liegt darin, dass beim Anzupfen einer Saite kurzzeitig eine Dreieckskonfiguration und demzufolge eine Knickfunktion entsteht. Wie sollte daraus überhaupt eine harmonische Schwingung hervorgehen und wie konnten auf der Saite zugleich mehrere Harmonische schwingen?
Im Beispiel der gezupften Saite ist die Anfangsgeschwindigkeit Null, so dass gilt:
y(x, t) = (1/2)[F(x - ct) + F(x + ct)]
Ohne die Verwendung von Fourierreihen ein vermutlich kaum zu bewältigendes Problem.
Erste Klärung der Begriffe:
1) Unter einer diesbezüglichen Schwingung versteht der Fachmann eine periodische Auslenkung einer Masse (Feder, Fadenpendel, Saite) aus ihrer Ruhelage. Dabei wandelt das System seine kinetische Energie abwechselnd in potentielle und wiederum in kinetische um. Im Unterschied zu einer Welle handelt es sich um ein räumlich begrenztes und zeitliches Phänomen.
2) Unter einer Welle wird dagegen eine sich im Raum oder auch in Materie ausbreitende Oszillation verstanden, deren Schwingungsrichtung von der Beschaffenheit des Mediums (Aggregatzustand, Geometrie) abhängig ist. Einem derartigen von der Quelle sich ablösenden Wellenzug kann ein Impuls und eine Energiedichte zugeordnet werden.
3) Charakteristische Grössen einer Schwingung:
- Elongation y(t): momentane Auslenkung aus der Ruhelage
- Amplitude y_o bzw. A: maximale Auslenkung (Schwingungsweite)
- Periodendauer T: Dauer eines vollständigen Schwingungsvorganges
- Frequenz f: Anzahl Schwingungen pro Zeiteinheit
Die einfachste zu untersuchende Schwingung ist die harmonische, bei der die Rückstellkraft stets proportional zur Elongation ist (und somit ein lineares Kraftgesetz gilt):
y(t) = A*sin(ωt + φ_o)

Die Frequenz derartiger Sinusschwingungen ist unabhängig von ihrer Amplitude. Sind an der Erregung mehrere Kräfte beteiligt, erfolgt eine Überlagerung (Superposition) der Kräfte.
Für die Gesamtkraft lässt sich im Kontext der folgende Ausdruck entwickeln:
F = mω²y(t) = -Dy(t)
Der Proportionalitätsfaktor D wird als "Richtgrösse" bezeichnet (bei einer Feder die sog. Federkonstante).
Ohne fortlaufende Erregung klingt jede sich selbst überlassene Schwingung infolge der unvermeidlichen Reibung und Dissipation mit der Zeit ab.
Die Bewegungsgleichung (mit R als Reibungskoeffizient) lautet somit:
my'' + Ry' + Dy = 0
Es gilt für die Abklingfunktion:
y = A*e^(-kt)
Solche gedämpft verlaufende Schwingungen werden auch als "freie Schwingungen" bezeichnet. Die Frequenz der freien Schwingungen ist die Eigenfrequenz des Schwingers. Weil Eigenschwingungen energetisch günstigen Gesichtspunkten genügen, gilt: Je höher die Frequenz, desto geringer die Amplitude. Soll die Schwingung aufrecht erhalten werden, muss dem System periodisch Energie zugeführt werden. Solche Schwingungen werden als "erzwungene Schwingungen" bezeichnet; deren Amplitude wächst mit Annäherung an die Eigenfrequenz an und wird im Resonanzfall maximal. Im Extremum kann es zur sog. Resonanzkatastrophe kommen (Beispiel Tacoma-Narrows-Bridge, 1940), bei der mechanische Zerstörung die Folge ist.
4) Als einem der ersten in die zu untersuchende Problematik involvierten Mathematiker gelang es Brook Taylor (nach welchem die Taylorreihen benannt sind) eine für die schwingende Saite griffige Formel zu finden, die auch dem Instrumentenbauer in praxisgemässer Form geläufig ist. Taylor berücksichtigte dabei nur die sinusförmige Grundschwingung bzw. die Halbschwingung des Grundzustandes der Saite:
f = (1/2l) * sqrt(F/ρA)
ρA --> Masse pro Längeneinheit
Demzufolge gilt:
Bei gleichbleibender Frequenz und Verdoppelung der Saitenlänge muss auch die Zugkraft verdoppelt werden (ohne dass freilich der Zargen oder sonstwas reisst) - äquates gilt auch bei Verdopplung der Saitenmasse. Als Materialien kommen Metalldrähte (Stahl, Bronze) oder Darm - heutzutage auch Kunststoffschnüre - in Betracht. Für tiefe Töne werden bewusst dicke Saiten gewählt (wie dies von der Bassgitarre bekannt sein dürfte). Weitere Komplikationen zum Problem (wie Biegesteifigkeit der Saite, Nichtlinearität der Saitenschwingungen und Rotationsträgheit der Saitenelemente) konnten zu Taylors Blütezeit noch nicht behandelt werden.
Nebst dem obig berechneten Grundton kommen real immer auch Obertöne (seltener Subharmonische) vor, die das charakteristische Klangbild mitbestimmen. Es bilden sich entlang der Saite Schwingungsmoden mit feststehenden Schwingungsknoten aus. Die Schwingungsperiode einer tieferen Mode ist stets ein ganzzahliges Vielfaches einer höheren Mode.
Weitere Klarheit auf dem dornigen Pfad der Erkenntnis erbrachte die Wellengleichung von d'Alembert:
∂²u/∂t² = c²(∂²u/∂x²)
u(x, t) --> Auslenkung der Saite am Ort x zur Zeit t
c --> positive Konstante, Ausbreitungsgeschwindigkeit der auf der Saite entstehenden Welle
(Für Wellen in flachem Wasser muss man stattdessen die Korteweg-de-Vries-Gleichung bemühen.)
5) In der Folge trug Euler mit seinen Arbeiten "Über Kettenbrüche" (1737) und "Über die Schwingungen einer Saite" (1748) zur Lösung des uralten Problems bei, indem er gedanklich die Eigenschwingungen eines mit Perlen besetzten masselosen elastischen Fadens untersuchte.
Daniel Bernoulli stellte den Satz auf, dass die Lösung des Problems der frei schwingenden Saite als trigonometrische Reihe darstellbar ist.
Der sich daraus ergebende Disput zwischen Euler, d'Alembert und Bernoulli erstreckte sich über Jahrzehnte. Eigentlich eine Satire und an sich unnötig, ganz im Sinne von: Keiner will die Formeln des anderen lesen.
Danach gelang Lagrange der entscheidende Beleg, wie man durch Grenzübergang von der Lösung des Problems der Schwingungen einer Perlenschnur zur Lösung des Problems der Schwingungen einer homogenen Saite gelangt.
Siehe dazu u.a.:
Szabo, Geschichte der mechanischen Prinzipien (Birkhäuser)
6) Den Abschluss dieser Entwicklung bildete Fourier (1822) mit seiner Untersuchung über die Wärmeausbreitung in Festkörpern (Théorie analytique de la chaleur). Die von Fourier dazu benutzten trigonometrischen Reihen werden als Fouriereihen bezeichnet und die diesbezügliche Analyse als Fourieranalyse. Es lässt sich nachweisen, dass jede periodische Funktion als eine Summe von Sinus- und Kosinusfunktionen darstellbar ist. Dies war der Schlüssel zur Erweiterung der erforderlichen Kenntnisse. Fortan konnten schier beliebige Schwingungen (Klänge) in ihre spektrale Zusammensetzung zerlegt werden. Der Weg von Pythagoras Monochord bis zur mathematischen Beherrschung der schwingenden Saite war in der Tat ein weiter.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 13.08.2009, 03:57 Titel: Verfasst am: 13.08.2009, 03:57 Titel: |
 |
|
Nachtrag II
Zu schwingenden Flächenhäuten (Erweiterung der Wellengleichung in 2 Dimensionen unter Beizug des Laplace-Operators).
Im Vorbeitrag lag der Schwerpunkt auf der schwingenden Saite (schwingende Stäbe wurden nicht behandelt). Jetzt sollen schwingende Flächen in den Vordergrund rücken.
Hilfsmittel:
Korsch, Mathematische Ergänzungen zur Einführung in die Physik (Binomi Verlag)
Allgemeines:
Bei einer schwingenden Membran handelt es sich um eine ansonsten schlaffe, nun aber unter Zugspannung σ stehende Haut. Diese verkörpert das zweidimensionale Analogon der schwingenden Saite. Demzufolge muss die Wellengleichung umgeschrieben werden in eine partielle Differentialgleichung in x, y und t. Dies gelingt unter der Voraussetzung, dass die partielle Ableitung ∂²u/∂x² durch den Laplace-Operator Δu ersetzt wird, somit:
Δu = ∂²u/∂x² + ∂²u/∂y² = (1/c²) ∂²u/∂t²
u --> Auslenkung senkrecht zur Membran
Die Ausbreitungsgeschwindigkeit c wird durch die Materialkonstante der Membran bestimmt: c = √(σ/ρ)
Um die Schwingungen eines elastischen Mediums (Membrane) im Dreiraum zu beschreiben, wird die Wellengleichung in modifizierter Form bemüht:
Δu - (1/c²) ∂²u/∂t² = 0
u(x,y,z,t) --> Amplitude
A) Gedankliche Anreize ohne feststehende Lösungen:
A1) Gegeben sei eine an den Rändern fest eingespannte kreisrunde Membran einer Trommel, die gegen die Mitte leicht nach aussen gewölbt ist. Zur Behandlung der Problematik verwenden wir eine Prozedur, welche die Laplace-Gleichung erfüllt - mit dem eklatanten Unterschied, dass anstelle des ansonsten üblichen Differentialoperators ein Differenzenoperator vorkommt:
ϑ²u/ϑx² + ϑ²u/ϑy² = 0
u --> Höhe über der (x,y)-Ebene
(als Randwerte nehmen wir u=0 für den äusseren und u=1 für die Innenzone an)
Damit lässt sich die Membranfläche mittels CAS oder dazu geeigneter Standardprogramme modellieren.
B) Gehen wir nun zu flächenhaften Kontinua mit Lösungsansatz über:
B1) Für den hier betrachteten Sonderfall einer kreisförmigen Membran wird der Laplace-Operator mit Vorteil in Polarkoordinaten r und φ dargestellt.
Lösen lässt sich die diesbezügliche Dgl. mit dem Bernoulli-Ansatz:
u = Ψ(r,φ) • sin ωt
Bei vollständiger Kreissymmetrie der Membrane folgt daraus eine gewöhnliche Differentialgleichung für Ψ(r) mit homogenen Randbedingungen. Mittels diesen lässt sich die Lösung durch Besselfunktionen angeben:
Ψ(r) = k * J_n(r) ; k = const.
Die Erfüllung der 2. Randbedingung Ψ(R) = 0 liefert für kreisförmige Knotenlinien die Eigenwerte der Schwingungen kreisförmiger Membranen. Deren Frequenzen sind proportional den Nullstellen y_0,m der Besselschen Funktionen:
f_0,m = (y_0,m/2π)(1/R) • √(σ/ρ)
(m = 1, 2, 3, ... steht für die Anzahl kreisförmiger Knotenlinien (Moden) auf der Membran)
Kreismembrane mit Knotenlinien:

Allgemeine Lösungen stellen Eigenfunktionen Ψ = (r,φ) mit kreisförmigen als auch geradlinigen Knotenlinien.
B2) Gegeben sei eine an den Rändern fest eingespannte Rechteckmembran mit den Seitenlängen a und b (bzw. den Koordinaten x und y). Die Auslenkung u senkrecht zur (x,y)-Ebene soll der zweidimensionalen Wellengleichung genügen.
Zudem soll gelten:
u(x = 0,y,t) = u(x,y = 0,t) = u(x = a,y,t) = u(x,y = b,t) = 0
Zur Lösung der Wellengleichung wird ein Separationssatz angewandt (mit den sich daraus ergebenden Linearkombinationen von Sinus- und Kosinusfunktionen) - somit:
u(x,y,t) = A sin px • sin qy • cos(rct + a)
(damit werden die Randbedingungen bei x = 0 und y = 0 erfüllt)
Die Bedingungen lauten dann:
p = mπ/a ; m = 1, 2, 3, ... ; q = nπ/b ; n = 1, 2, 3, ...
Die Frequenzen der Eigenschwingungen berechnen sich dadurch wie folgt:
u(x,y,t) = A sin(mπx/a) • sin(nπy/b) • cos(ω_m,n t + φ)
Für die unteren Eigenfrequenzen einer Rechteckmembran mit a = (√2)b gilt dann:
ω_m,n/ω_1,1 = √(m² + 2n²/3) mit m,n = 1, 2, 3, ...
Die Schwingungsmoden gleichen in diesem Fall einem mit der Dauer 2π/ω_m,n alternierenden Schachbrett mit abwechselnd positiven und negativen Auslenkungen. Bestimmte Moden sind mit sog. Entartungen behaftet, d.h. dass deren Eigenfrequenzen gleich gross ausfallen.
Schwingungsmoden einer Rechteckmembran:

In Summe kristallisiert sich immer deutlicher heraus, dass die "Physik der Musikinstrumente" ohne den Einsatz der höheren Mathematik ein hoffnungsloses Unterfangen bliebe. Aus diesem Grunde dauerte es auch so lange, bis die damit assoziierten Probleme eine Lösung fanden. Die ansonsten hervorragenden Kenntnisse der alten Geometer aus dem Orient reichten dazu schlichtweg nicht aus.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 13.08.2009, 07:13 Titel: Verfasst am: 13.08.2009, 07:13 Titel: |
 |
|
Nachtrag III
Zu schwingenden Stäben (Zungen) und schwingenden Platten.
A) In schwingenden Stäben kommen unterschiedliche Schwingungen resp. Wellen vor:
1) stehende Dehnwellen
2) stehende Torsionswellen
3) stehende Biegewellen
A1) Dehnwellen:

Die Eigenfrequenzen berechnen sich für a (beidseitig eingespannt) und c (beidseitig freie Enden) mit:
f = (n + 1/2l) • sqrt(E/ρ)
Anm.: Die Eigenfrequenzen des freien Stabes sind völlig unharmonisch; man versuche sich an den charakteristischen Klang des Glockenspiels (bestehend aus einer Reihe meist rechteckiger Stahl- oder Aluminiumstäbe) mit seinem harten und etwas klirrenden Ton zu erinnern. Bei anderen Stabspielen (Marimba, Xylophon und Vibraphon) werden die Eigenfrequenzen durch Auskehlung des Stabes in ein näherungsweise harmonisches Verhältnis gebracht.
Für b (einseitig eingespannt) gilt:
f = (2n + 1/4l) • sqrt(E/ρ)
E --> Elastizitätsmodul
n = 0, 1, 2, 3, ...
n0 --> Grundschwingung (1. Harmonische)
n1, n2, n3, ... --> Oberschwingungen (n-te Harmonische)
A2) Torsionswellen:

Analog zu den Dehnwellen gilt hier:
f = (n + 1/2l) • sqrt(G/ρ)
f = (2n + 1/4l) • sqrt(G/ρ)
G --> Schermodul
A3) Biegewellen:

In biegesteifen Stäben bilden sich bei entsprechender Anregung stehende Transversalwellen aus.
Die Biegefrequenz berechnet sich mit:
f = (α²/l²)(l/2π) • sqrt(El/ρA)
Die α-Werte (Eigenwerte) sind von den Randbedingungen abhängig und einem entsprechenden Tabellenwerk (z.B. Dubbel, Taschenbuch für den Maschinenbau) zu entnehmen.
B) Dünne isotrope und biegesteife Platten sind die zweidimensionale Erweiterung des linearen Stabes (Schalen und Glocken diejenige eines gekrümmten Stabes).

Stillschweigend soll gelten: Massensichte ρ = dm/dV = const.
Es sind folgende Randbedingungen zu unterscheiden: frei, einfach unterstützt und eingespannt.
B1) Nebst longitudinalen und transversalen Wellen (nicht-dispersiv; keine signifikante Schallabstrahlung) treten Biege- oder Verformungswellen (dispersiv; signifikante Schallabstrahlung) in Erscheinung.
B1a) Geschwindigkeit longitudinaler Wellen in unendlich ausgedehnten Platten:
c_l = sqrt(E/ρ(1 - v²))
B1b) Geschwindigkeit longitudinaler Wellen in dünnen Platten:
c_l = sqrt(E(1 - v²)/ρ(1 + v)(1 - 2v))
B1c) Geschwindigkeit transversaler Wellen in unendlich ausgedehnten flachen Platten:
c_t = sqrt(G/ρ) ≈ 0.6 c_l
B1d) Phasengeschwindigkeit von Biegewellen:
c_ph = ω/k = (c_l * h/√12)k
B1e) Gruppengeschwindigkeit von Biegewellen:
c_gr = ∂ω/∂k = 2 * v_ph
B2) Ein im Allg. schwieriges Problem ist die math. Behandlung dünner Rechteckplatten. Bei einfacher Unterstützung entstehen kreisförmige Knotenlinien (m,n) wie bei der Membran. Bei veränderten Randbedingungen entstehen durch Mischung der (m,n)- und (n,m)-Moden auch gekrümmte Knotenlinien. Schwingende rechteckige Platten dienen als Modell für Decke und Resonanzboden von Musikinstrumenten (Violine, Bratsche, Gitarre).
B3) Bei quadratischen Platten sind dem Schreiberling ausser den Fundamentalmoden zahlreiche weitere Moden und Knotenlinien als "Chladnische Klangfiguren" bekannt. Die frei schwingende quadratische Platte dient als Modell für den Biegewellenwandler (DML) in der Lautsprechertechnik.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 13.08.2009, 14:32 Titel: Verfasst am: 13.08.2009, 14:32 Titel: |
 |
|
Nachtrag IV
Zu Röhren- und Helmholtzresonatoren (akustische Schwinger ohne bewegliche Teile).
A) Röhrenresonatoren kommen insbesondere für Blasinstrumenten in Betracht. Konstruktiv werden sie wahlweise mit einem geschlossenen und einem offenen Ende oder mit zwei offenen Enden gebaut. Die tieferen Eigenfrequenzen der Röhre erzeugen durch Wechselwirkung mit dem Tonerzeuger (Rohrblatt, Lippen) die für das jeweilige Instrument charakteristischen Töne. Die höheren Eigenfrequenzen wirken als akustisches Filter und bestimmen die individuelle Klangfarbe.
Röhrenresonator (Prinzip):

Quelle: Görne, Tontechnik (Hanser)
- links: λ/2-Resonator (beidseitig offen) mit allen harmonischen Teiltönen
- rechts: λ/4-Resonator (einseitig offen) mit ungeradzahligen Teiltönen
A1) Das beidseitig offene zylindrische Rohr ist ein Modell für sämtliche Flöten (Blockflöte, Querflöte) und für die offenen labialen Orgelpfeifen. Beim Bau eines realen Instrumentes ist die Mündungskorrektur zu berücksichtigen. Die Eigenfrequenzen stehen im Verhältnis 1:2:3:4...
A2) Das einseitig geschlossene Rohr besitzt an seinen beiden Enden unterschiedliche Randbedingungen. Es dient als Modell für Klarinette und gedeckte Orgelpfeife. Am offenen Ende muss ein Schalldruckknoten erscheinen, am geschlossenen Ende ein Schalldruckmaximum. Auch hier muss die Mündungskorrektur berücksichtigt werden. Die Eigenfrequenzen stehen im Verhältnis 1:3:5:7...
A3) Komplizierter als das zylindrische ist das konische Rohr. Es ist ein Modell für Oboe und Fagott. Obwohl einseitig geschlossen, ist es ein λ/2-Resonator zur Bildung von Kugelwellen-Abschnitten.
A4) Der bei den meisten Blasinstrumenten vorkommende Schallbecher - als Aufweitung am Rohrende - macht das akustische Verhalten noch erheblich komplizierter. Das einseitig geschlossene Rohr mit Schallbecher dient als Modell für Trompete und Posaune, das konische Rohr mit Schallbecher für Horn und Flügelhorn und in speziellem Sinne für das Saxophon.
B) Etwas anders funktioniert der Helmholtz-Resonator (als akustisches Analogon zum Masse-Federpendel).
Helmholtzresonatoren unterschiedlicher Eigenfrequenzen:
http://sites.google.com/site/futurephysics/Home/helmholtz_resonator_1.jpg
Konstruktiv sind kugelförmige als auch quaderförmige Resonatoren denkbar. Entwickelt wurde dieses verschleissfreie Gerät vom Physiker und Physiologen Hermann von Helmholtz (1821-1894) für die akustische Spektralanalyse.
Die Luft in der kleinen Öffnung wirkt als schwingende Masse, das eingeschlossene Luftvolumen wie eine Feder.
Prinzip des Helmholtzresonators:

Wie beim Masse-Federpendel existiert auch beim Helmholtz-Resonator eine ausgeprägte Eigenfrequenz, die von den geometrischen Abmessungen und Systemparametern abhängig ist:
ω = sqrt(K/M)
K --> Federkonstante
M --> träge Masse
Bestimmung der Resonanzfrequenz:
f = (c/2π) • sqrt(A/l_eff * V)
A --> Querschnittsfläche an der Öffnung des Resonatorhalses
l_eff = 2Δl (l = Länge des Mündungshalses)
Im Resonanzfall ist die vom Resonator aufgenommene Schallenergie maximal.
Um die effektive Mündungstiefe zu bestimmen (die Luft schwingt auch ausserhalb des Resonators) ist eine Mündungskorrektur an den Enden des Resonatorhalses um 2Δl erforderlich.
In seiner Wirkung entspricht der Helmholtz-Resonator einem Tiefpassfilter. Anwendungen finden sich als Schallabsorber schmalbandiger, tieffrequenter Raummoden und als Schallverstärker (Gitarren- und Klavierkorpus); aber auch, um Schall abzustrahlen (Bassreflexbox) oder zu filtern (Bandpassbox).
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 14.08.2009, 23:19 Titel: Verfasst am: 14.08.2009, 23:19 Titel: |
 |
|
Nachtrag V
Zu Glocken und Zimbeln...
Steh, Wanderer, still! Denn hier entstand,
daß keine zweite möglich werde,
gebaut durch Schillers Meisterhand,
die größte Glockenform der Erde.
Glocken waren bereits im alten China der Schang-Dynastie bekannt. Durch Wandermönche kamen die Glocken im 2. Jh. auch nach Europa. Das Cymbalum (Klangschalen, Becken) aus Bronze oder Messing war zu Zeiten des Königs David in Israel verbreitet. Bekannt sind uns Heutigen die Tam-Tams (ein Metallgong, gewöhnlich durch mit Filz überzogene hölzerne Klöppel geschlagen), von Mussorgski in "Eine Nacht auf dem Berge" als dramaturgisches Element eingesetzt. Und wer von den Aelteren unter uns kennt nicht den Schellenbaum, ein effektvolles in militärischen Marschzügen eingesetztes Instrument.
A1) Glocken sind im einfachsten Falle gekrümmte Platten und das flächenhafte Gegenstück einer Stimmgabel. Treicheln (Kuhglocken) werden aus Blechen gewalzt und geschmiedet und in Maschinen geformt.
Handgeschmiedete Treichel:
http://sites.google.com/site/futurephysics/Home/treichel.jpg
Etwas kleiner - und damit leichter - sind die Weideschellen der Kühe. Den Pferden werden bei festlichen Anlässen zuweilen kleine Glocken (Kummetrollen) angehängt. Bekannt sind die vernickelten Kreuzrollen.
A2) Bei den gegossenen Glocken besteht die Kunst darin, durch die Formgebung (Rippe) und Dicke der Wandung möglichst viele harmonische Obertöne zu erzielen. Dünnwandige Glocken klingen tiefer als dickwandige. Bewährt hat sich die "gotische Rippe" (Glockenhöhe ohne Krone = Schärfendurchmesser). Die abendländischen Glocken aus dem 9. Jh. hatten eine bienenkorbähnliche Form und klangen eher dumpf. Mitte des 12. Jh. zeichnete sich ein Wechsel zur zuckerhutförmigen Glocke mit schmaler Flanke und ausladendem Wolm ab, welche einen froheren Klang aufweist. Zu Beginn des 13. Jh. entstand dann sukzessive die gotische Rippe. Insbesondere die gotische Dreiklangrippe aus dem 14. Jh.dient den Glockengiessern noch heute als Vorbild. Als Gusswerkstoff - "Glockenspeise" genannt - wird meist Zinnbronze (eine Legierung aus 78 % Kupfer und Zinn) verwendet.
Eine schöne Glocke zu giessen wäre auch mein Wunsch. Wer bringt es mir bei?
Moderne Bronzeglocke (Kirchenglocken haben einen Namen):
http://upload.wikimedia.org/wikipedia/de/f/f3/Glocke_von_2005.jpg
Eine nicht geringe Bedeutung bezüglich der Klangqualität kommt dem Klöppel aus Weicheisen oder Stahlguss zu. Zu hart darf er nicht sein. Glocke und Klöppel bilden ein Doppelpendel. Beim Läuten schlägt der Klöppel mit dem sog. Ballen auf dem Schlagring der Glocke auf. Es entstehen Biegschwingungen im Glockenmantel. Entlang des Umfanges sind stehende Wellen zu beobachten und auf der Oberfläche entstehen Knotenlinien.
Schwingungsmoden einer Glocke:

Nach Fletcher und Rossing, The Physics of Musical Instruments (1991)
Beim Anschlag des Glockenkörpers nimmt man den Schlagton (Nominal) wahr, der nicht in der Glocke selbst, sondern erst im Ohr als Kombinationston (?) entsteht. Das Ohr erkennt den fehlenden Grundton und empfindet diesen als Anschlagnote. Oft sind die Obertöne zum Grundton nicht harmonisch. Auch erklingen Unteroktave, Prime, kleine Terz, Quinte und Oberoktave. Man unterscheidet zwischen Prinzipalton- und Mixturbereich. Non- und Septimglocken gibt es freilich auch.
Es gab der Legende zufolge eine Glocke auf dem Kölner Dom, die einfach nicht läuten wollte. Grund dafür war, dass Klöppel und Glocke synchron schwangen, so dass der Klöppel nie auf den Schlagring stiess. Wie konnte man dieses Problem lösen ohne die Glocke vom Glockenturm zu holen? Nun, der Klöppel wurde verlängert und dadurch schwerer gemacht. Als ihn dann die Glocke traf, folgte er dieser wegen seiner grösseren Trägheit nicht länger synchron, so dass die hin und her schwingende Glocke ihn periodisch schlagen konnte.
In den vergangenen Jahren war ich nicht in Köln. Das Verklingen der "Pretiosa" im Kölner Domgeläute soll aber ein akustischer Genuss sein.
B1) Zur Wahrnehmung der Glockentöne
Der dominant empfundene Ton wird als Schlag- oder Nominalton bezeichnet. Es handelt sich um einen Residualton, weil er keiner Eigenschwingung der Glocke entspricht. Möglicherweise wird dieser Ton im Gehirn - zumindest aber im Innenohr - erzeugt. Physikalisch ist er ausserhalb nicht nachzuweisen. Nach heutiger Erkenntnis werden die Residualtöne in einem festgelegten Band der Basilarmembran aus den dort registrierten Obertönen abgeleitet. Bereits Schouten (der Begründer der Residuumtheorie) konnte nachweisen, dass sie sich von den durch Nichtlinearität erzeugten Helmhotzschen Kombinationstönen unterscheiden und durch Interferenz nicht ausgelöscht werden.
H. Riemann (1916) vermerkt dazu:
| Zitat: | | ...daß das Musikhören nicht nur ein passives Erleiden von Schallwirkungen im Hörorgan, sondern vielmehr eine hochgradig entwickelte Betätigung von logischen Funktionen des menschlichen Geistes ist... |
Seebeck seinerzeit hatte im Zuge seiner Lochsirenenexperimente folgende Schlussfolgerung gezogen:
| Zitat: | | Das Ohr empfindet den Eindruck einer periodischen Bewegung als Ton; alle Glieder, welche an dieser Periode Theil nehmen, können [...] zur Stärke des Tons beitragen. |
Fazit:
Sind genügend Obertöne vorhanden, vermag das menschliche Klangsensorium den (fehlenden) Grundton zu erkennen.
B2) Aus einem meiner geistigen Elaborate (die oft im Dunkel der Nacht entstehen):
Ohm, der das Fouriertheorem auf die Akustik übertrug, hatte bereits früh Kritik an Seebeck's These der Tonbildung durch Periodizität einer Pulsfolge geübt, indem er festhielt, dass bei einer sinusförmigen Schwingung immer diejenige Tonhöhe als Grundtonhöhe wahrgenommen wird, die der Frequenz der Schwingung entspricht. Seebeck wiederum hielt fest, dass die Anwesenheit einer Sinusschwingung bestimmter Frequenz nicht grundlegend zum Hören einer Tonhöhe dieser Frequenz sei. Ohm ging jedoch davon aus, dass dieses Phänomen der "akustischen Illusion des Ohres" zuzuschreiben sei. Seebeck zeigte sich immerhin versöhnlich, indem er erklärte, dass die unterschiedliche Klangfarbe von Tönen gleicher Frequenz nur durch die Zerlegbarkeit der periodischen Schwingung in ihre Sinuskomponenten zu verstehen sei. Mit seinen Schlussfolgerungen hatte Seebeck das Residuum bereits ohne zu wollen vorweggenommen.
Auch Hermann (1890) kam zum Schluss, dass im Frequenzspektrum gesungener Vokale der Grundton oft nur sehr schwach vertreten ist, ungeachtet dessen aber immer wahrgenommen wurde. Aus seinen eigenen Experimenten - in Anlehnung an König's Unterbrechungstöne - schloss er, dass das das Ohr dazu fähig ist, periodische Schwankungen der Amplitude als Ton wahrzunehmen. Weitere Untersuchungen in diese Richtung stammten von Pipping, welcher feststellte, dass eine Gruppe von Harmonischen bereits ausreichte, um eine bestimmte Tonhöhe zu generieren. Er führte dieses Phänomen darauf zurück, dass der fehlende Grundton durch die nichtlineare Verarbeitung im Hörorgan wiederhergestellt wurde.
Fletscher (1924) vermochte auf elektronischem Wege nachzuweisen, dass eine beliebige aus dem "komplexen Ton" herausgenommene Reihe dreier aufeinander folgender Obertöne ausreichte, um eine deutliche Grundfrequenz hörbar zu machen. Auch er begründete diesen Sachverhalt mit der Hypothese, dass der fehlende Grundton durch das nichtlineare Übertragungsverhalten des Ohres bestimmt wird.
Widerlegt wurde die Resonanztheorie von Helmholtz durch Békésy (Nobelpreis für Medizin, 1961). Zwar muss auch dessen Wanderwellentheorie aus moderner Sicht als ungenügend angesehen werden. Sie wurde durch eine zelluläre Verstärkertheorie (Cochlear-Amplifier) abgelöst.
In neueren Studien kommt Plomb zum Schluss, dass die eindeutig wahrnehmbare Tonhöhe eines komplexen Tones nicht von der Anwesenheit des Grundtones abhängt, sondern dass dem Gehör vielmehr durch die Periodizität eines Signals die primäre Voraussetzung zur Wahrnehmung des Grundtones gegeben ist.
Gegenüber diesen Vorstellungen gehen die Verfechter des "Pattern Recognition Modells" davon aus, dass es sich beim Residualton in erster Linie nicht um eine aus der Gesamtperiode einer Schwingung abgeleitete Wahrnehmung handelt, sondern um das Produkt eines angelernten Mustererkennungsprozesse. Allerdings versagt dieses Modell zunächst bei der quantitativen Betrachtung der simultanen Repräsentation zweier Residualtöne. Bei der Kombination zweier Residualtöne entsteht nämlich immer ein dritter Residualton, der sich aus der Gesamtperiode der Ausgangstöne ergibt. Liegt dieser resultierende Residualton nicht tiefer als die anderen zwei Residualtöne, wird er immer sehr deutlich wahrgenommen.
Offensichtlich ist das "Periodicity pitch Modell" - welches die wahrgenommenen Tonhöhen aufgrund der Periodizität des aus den Obertonreihen resultierenden Signals ableitet - auf den ersten Blick realitätsnaher aufgebaut.
Langer bspw. hat nachgewiesen, dass es bestimmte Klassen von Neuronen in der Hörbahn gibt, die wie eine Korrelationsanalyse arbeiten. Jüngste Untersuchungen im Rahmen des "Korrelationsmodells" befassen sich mit der neuronalen Weiterverarbeitung des vom Hörnerv stammenden Erregungspotentials. Nach Langer (1997) reagieren Neuronen im 'Colliculus inferior' häufig auf Signale, die in harmonischer Beziehung zueinander stehen.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|