| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 17.06.2008, 04:49 Titel: Techno-Aphorismen Verfasst am: 17.06.2008, 04:49 Titel: Techno-Aphorismen |
 |
|
Interessant manchmal, wie nahe der Dichter der Wahrheit kommt:
Gelehrte sahen mit erstaunten Augen,
Dass kleine Flöhe an den - Flöhen saugen,
Die wieder quält noch kleinere Kreatur -
So geht ins Ungemess'ne die Natur.
aus "Eine Rhapsodie" von Swift (1733)
Man darf nur hoffen, dass diese Satzellipse adäquat übersetzt wurde.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 17.06.2008, 23:17 Titel: Verfasst am: 17.06.2008, 23:17 Titel: |
 |
|
Der Clou bei Swift ist folgender:
Ein (Horn)-Ochse mag von einem gemeinen Floh gepeinigt werden; doch die Flöhe eines Flohs werden in kaum stören, weil winzige Grössen zweiter Ordnung einfach zu unbedeutend sind. So die Volksmeinung.
Damit ist das Thema einer zweimal stetig differenzierbaren Funktion hinreichend umrissen.
Geometrisch gesehen ist die zweite Ableitung mit der Krümmung in einem bestimmten Punkt des Graphen identifizierbar (Krümmung als "Steigung der Steigung"). Manchmal tut es gut, zu wissen, wie die Funktion verläuft. Linksgekrümmt nennt sich die Funktion mit zunehmender Tangentensteigung, rechtsgekrümmt mit abnehmender. An Polynomen bspw. lässt sich das Gesagte gut untersuchen.
Aendert sich das Krümmungsverhalten, spricht man von einem Wendepunkt. Der Ausdruck "Wendetangente" ist dem Regelungstechniker ein Begriff. So lässt sich bekanntlich die Anstiegszeit einer Übergangsfunktion mittels Wendetangentenkonstruktion ermitteln. Genial einfach!
Selbstverständlich gibt es auch die Approximation nach Küpfmüller. Der Praktiker wird sich an die Einstellregeln von Ziegler und Nichols für den Reglerentwurf halten. Der Erfolg gibt ihm recht.
Fazit:
Flöhe sind nicht immer unnütze Dinger!
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 18.06.2008, 14:21 Titel: Verfasst am: 18.06.2008, 14:21 Titel: |
 |
|
Zu den Ableitungen 1. und 2. Ordnung (Flöhe von Flöhen):
In der Regelungstechnik gibt es einige besonders interessante Funktionen. Dazu gehören die Knickfunktion, die Heavisidefunktion und die Diracfunktion. Der Mathematiker spricht von Distributionen. In praxi reden wir weiterhin von Funktionen; für uns gibt es keine idealen Kurvenzüge, sondern nur Approximationen. Diese Freiheit nehmen wir uns. Die mathematischen Feinheiten überlassen wir den Gralshütern der Wissenschaft.
Beispiele:
Der Anstieg einer Heaviside- oder Sprungfunktion verläuft nie in Nullzeit. Wer ein Speicheroszilloskop sein eigen nennt und die Zeitbasis entsprechend justiert, sieht den realen Verlauf. Ebenso gibt es in praxi keinen unendlich schmalen Impuls. Die Dirac- oder δ-Funktion kann aber durch einen Nadelimpuls realisiert werden. Klatsche kurz und scharf in die Hände und du erzeugst einen Diracstoss mit dem vollen Frequenzspektrum!
Alles beginnt mit einer Stammfunktion F(x):
Die 1. Ableitung der Knickfunktion ist die Heavisidefunktion:
d/dx K(x - ξ) = Θ(x - ξ)
Die 2. Ableitung der Knickfunktion ist die Diracfunktion:
d^2/dx^2 K(x - ξ) = δ(x - ξ)
Der Empiriker benötigt diese Funktionen, um sein System zu testen. Gibt er ein Testsignal an den Reglereingang, kann er schauen, was hinten herauskommt. Zumindest weiss er bereits, was herauskommen sollte. Damit ist bereits viel gewonnen. Aber es benötigt eine gewisse Erfahrung, um die Reglerantwort angemessen zu interpretieren.
p.s.
Es ist ein Unterschied, ob einer den Regler entwirft oder ob einer die Anlage (Regler und Regelstrecke) einfährt. Für die Konzeptionierung eines Reglers hat sich die modellbasierte Simulation (Simulink/Stateflow/LabView) bewährt. Keiner rechnet dazu von Hand mit Differentialgleichungen; dafür gibt es erprobte Mathematiksoftware wie Matlab oder Mathcad. Man muss das Rad nicht immer wieder neu erfinden.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 13.07.2008, 23:52 Titel: Verfasst am: 13.07.2008, 23:52 Titel: |
 |
|
Analysis für Praktiker
1 - Differentiation:
In der Impulstechnik haben wir es vielfach mit Rechteckimpulsen zu tun. Ein idealer Rechteckimpuls hat lotrechte Flanken. In realiter haben Rechteckimpulse aber immer steile Flanken, denen in jedem Punkt eine bestimmte Steigung zukommt. Eine Sonderstellung besitzen die Distributionen. Differenziert man eine Heavisid'sche Sprungfunktion, erhält man einen Dirac'schen Deltaimpuls. Dieser wird als als sehr spitzer Nadelimpuls realisiert.
Solche Nadelimpulse werden technisch mittels RC-Gliedern (Hochpass) erzeugt. Bei richtiger Dimensionierung der Glieder (Zeitkonstante) verwandelt sich ein eingehender Rechteckimpuls in eine positive und eine negative "Impulszacke", die am Ausgang des Vierpols abgegriffen werden.
In der Fernsehtechnik benötigt man Differenzierglieder, um aus den Flanken der Zeilen-Synchronisierzeichen eine "Zackenreihe" zu bilden.
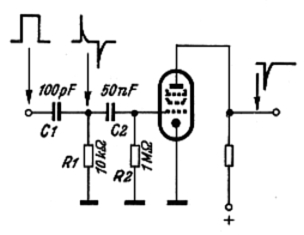
Werden nur die negativen Zacken benötigt, lässt man die Nadelimpulse durch das sog. Amplitudensieb laufen. Die positiven Zacken werden dabei weggeschnitten.
2 - Integration:
Wird als Integrierglied ein Tiefpass verwendet, kann auf einfache Weise eine Folge von Rechteckimpulsen aufintegriert werden. Dies macht man sich in der Fernsehtechnik zunutze, um die Bild-Synchronisierzeichen auf einen bestimmten Spannungspegel zu integrieren; damit lässt sich dann der Rastergenerator starten.
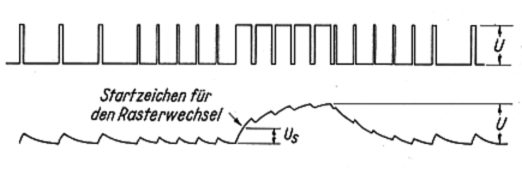
Um für den Beginn einer Integration einen entladenen Kondensator zu erhalten, laufen dem eigentlichen Bildsynchronisierimpuls sog. Trabanten voraus (das sind 5 sehr schmale Impulse). Gleiches geschieht nach dem letzten Rasterimpuls, um den Kondensator wieder vollständig zu entladen.
Der durch Integration gewonnene Spannungshub wird bei gewissen Geräten (Graetz) einer Auftaströhre zugeführt, die daraus "versteilerte" negativ gerichtete Spannungsspitzen erzeugt, die den Bildkippgenerator steuern.
3 - Differenzierer und Integrierer
3.1 In der Regelungstechnik benötigt man Differenzierer, um den D-Anteil zu bilden. In industrieelektronischen Schaltungen verwendet man dafür Operationsverstärker. Bestimmend sind der Rückkopplungswiderstand und der Kondensator.
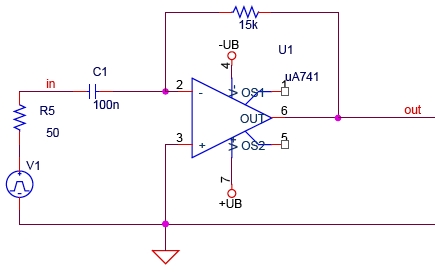
Ausgangsspannung: U_out = -RC(dU_in/dt)
3.2 Vertauscht man in der obigen Schaltung Widerstand und Kondensator, entsteht ein Integrierer. Die Spannung über dem Rückkopplungskondensator entspricht in etwa dem Integral des Eingangssignals. Hier ist das Integral in der Tat gleich der Fläche unter der Kurve.
Ausgangsspannung: U_out = (1/RC) Int U_in dt
Bekannt in Röhrenfernsehempfängern ist dem Eingeweihten der Miller-Integrator (auch als Miller-Transitron oder Phantastron bekannt). Dieser Integrator wird für die Vertikalablenkung benötigt, um die Sägezahnspannung zu generieren.
Eine weitere Anwendung des Integrierers ist der Dual-Slope-Wandler. Dieser wandelt ein analoges Eingangssignal in einen digitalisierten Wert um. Nutzung z.B. in DMM, um eine Spannung numerisch anzuzeigen.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|