| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
Aragorn
Anmeldedatum: 23.06.2006
Beiträge: 1120
|
 Verfasst am: 24.04.2009, 00:24 Titel: |
 |
|
| FrankSpecht hat Folgendes geschrieben: | | So, wie in deinem Beispiel, funktioniert das für ein bestimmtes Intervall. Die nicht-lineare Kurve unten wird aber in jedem Fall die lineare irgendwo in einem größeren Intervalls überholen. Das wäre wohl bei m*x = m*e^(m*x). Oder nicht? |
Deshalb habe ich ja auch nur den linken Bereich dargestellt. Ab x=23 wächst die e-Funktion schneller:
Ableitung der beiden Funktionen:
f1=m*x -> f1'=m
f2=m*e^(m*x) -> f2'=m^2*e^(m*x)
Gleichsetzen und nach x auflösen:
f1'=f2' -> x=1/m*lg(1/m)=23
-> ab x=23 ist die Steigung der e-Fkt größer.
Gruß Helmut |
|
| Nach oben |
|
 |
FrankSpecht
Anmeldedatum: 22.02.2006
Beiträge: 439
Wohnort: Oldenburg
|
| Verfasst am: 24.04.2009, 00:35 Titel: |
|
|
| Aragorn hat Folgendes geschrieben: | | Deshalb habe ich ja auch nur den linken Bereich dargestellt. Ab x=23 wächst die e-Funktion schneller |
Danke, hab' verstanden!
_________________
CS, Frank
http://www.rainbow-serpent.de/ |
|
| Nach oben |
|
|
ralfkannenberg
Anmeldedatum: 22.02.2006
Beiträge: 4788
|
| Verfasst am: 25.04.2009, 08:19 Titel: |
|
|
| richy hat Folgendes geschrieben: | Hi
Ja ich muss mich bei Ralf entschuldigen. Es gibt mathematisch kein Argument den Fall y(x)=0 auszuschliessen. |
Hallo richy,
selbstverständlich angenommen 
Weisst Du, es geht mir eigentlich weniger darum, wer sich bei wem zu entschuldigen hat, sondern welchen Eindruck der Laie, der hier mitliest, erhält: Dieser weiss, dass Du sehr kompetente Beiträge verfasst und schenkt dann solchen Beurteilungen von Dir Glauben.
Im übrigen habe ich nie bezweifelt, dass Du das richtige meinst und ich habe auch ein gewisses Verständnis, dass solche "Details" aus anwendungsorientierter Sicht oftmals als mühsam, als Hemmschuh empfunden werden. Das gilt für Physiker oftmals gleichsam wie für Ingenieure und - ich gebe das offen zu - auch für mich bis zu meinem 3.Semester, als mir damals die "Augen aufgingen".
Und auch in der Mathematik ist es üblich, sich bei einem Beweis zunächst auf seine Intuition und Erfahrung zu verlassen und all' diese Details als zutreffend vorauszusetzen. Aber nachdem dann der Beweis in seiner Rohform erbracht ist, geht es eben noch zur Knochenarbeit und alles muss hieb- und stichfest gemacht werden. Das hat dann oftmals zur Folge, dass der Beweis noch ergänzt werden muss, schlimmstenfalls hat das zur Folge, dass der ganze Beweis verworfen werden muss.
Ich denke, hier sollte ein disziplinenübergreifender Prozess genutzt werden und man sollte sich gegenseitig ergänzen: Die anwendungsorientierten Forscher, die eine grosse Erfahrung für praktische Anwendungen aufweisen, haben in der Regel wenig Lust, alles auf Konsistenz zu überpüfen, während die Mathematiker lieber in Strukturen und Analogien denken und meist wenig Lust haben, auch noch die Details anzuschauen.
Ich will das mit keinerlei Wertung verbinden, ich denke, beide Aspekte sind gleich wichtig !
Unter diesem Gesichtpunkt möchte ich nun nochmals die Aussage von Professor Rössler genauer beleuchten, ich tue dies aber aus Gründen der Übersichtlichkeit in einem eigenen Beitrag.
Freundliche Grüsse, Ralf |
|
| Nach oben |
|
|
ralfkannenberg
Anmeldedatum: 22.02.2006
Beiträge: 4788
|
| Verfasst am: 25.04.2009, 08:57 Titel: |
|
|
Hallo zusammen,
ich möchte mich nun nochmals mit der Aussage von Professor Rössler beschäftigen:
| Zitat: | | Nur eins ist sicher: nichtlinear ist immer "sehr viel" schneller als linear. |
In diesen wenigen Worten sind mindestens 4 Annahmen stillschweigend vorausgesetzt:
1.) stillschweigende Voraussetzung der Vorzeichen-Bereinigung
Wenn man eine exponentielle Funtion mit (-1) multipliziert, so wird sie nicht sehr schnell wachsen, sondern sehr schnell "fallen". Das hat aber nichts mit dem Wachstumsverhalten an sich zu tun und kann mit Vorzeichen-Bereinigung einfach abgehandelt werden.
Man beachte: aus "exponentiell" folgt nicht notwendig "Wachstum".
2.) die Wortwahl "schnell"
Wir haben gesehen, dass es nicht-lineare Funktionen gibt, die auch vorzeichenbereinigt langsamer als lineare Funktionen wachsen. Dazu gehören z.B. alle Wurzelfunktionen n.-ter Wurzel.
Man beachte: aus nicht-linear folgt nicht notwendig "schnelleres Wachstum".
3.) die Wortwahl "sehr viel"
In der Arithmethik wird oftmals der Begriff des linearen Wachstums durch den Begriff des polynomialen Wachstums verallgemeinert; sowas kommt bei Programmlaufzeit-Überlegungen zur Anwendung, wobei hier das Wort "Wachstum" durch "Laufzeit" zu ersetzen ist. - Polynome n.-ten Grades wachsen im Allgemeinen (d.h. für n > 1) schneller als lineare Funktionen; dennoch liegt kein exponentielles Wachstum vor.
Man beachte: aus (nicht-linear) .und. (schneller als linear-wachsend) folgt nicht notwendig "exponentielles Wachstum".
4.) endliche Intervalle
Das Wachstumsverhalten bezieht sich ja für grosse x und El Cattivo hat uns vorgestern freundlicherweise in seinem Beitrag von 14:03 Uhr darauf hingewiesen, dass in endlichen Intervallen durchaus möglich ist, dass eine exponentielle Funktion weniger rasch als eine lineare Funktion anwächst. El Cattivo hat dabei Regelvorgänge angesprochen, die in der Praxis eine Rolle spielen; ein Grund für eine solche Regelung ist beispielsweise die "Sättigung"; tatsächlich gilt dies nicht nur für Bakterienkulturen oder Kettenbriefe, sondern auch für LHC-artige Schwarze Löcher mit hypothetischem exponentiellen Wachstum: Wenn diese also tatsächlich exponentiell anwachsen, so werden sie irgendwann einmal die Materie des gesamten Universums akkretiert haben und dann ist das exponentielle Wachstum beendet und die Wachstumskurve flacht ab. Der Vollständigkeit halber sei erwähnt, dass das auch für beliebige Wachstumskurven gilt, nur dauert das dann entsprechend länger und entzieht sich entsprechend dem experimentellen Zugriff.
Man beachte: aufgrund der Randbedingungen kann es möglich sein, dass "exponentielles Wachstum" nicht für beliebig grosse x aufrechterhalten werden kann.
Wenn man hier als nicht aufpasst, könnte man einen - unzutreffenden - "Beweis" konstruieren, dass Weltmodelle mit endlicher Masse (u.a. das Urknallmodell) falsch seien; diese Thematik ist heutzutage ja wieder in Mode gekommen. Ich finde es aber schade, wenn man zu Resultaten gelangt, die falsch sind, nur weil man z.B. vergessen hat, endliche Intervalle zu berücksichtigen.
Freundliche Grüsse, Ralf |
|
| Nach oben |
|
|
El Cattivo
Anmeldedatum: 22.04.2007
Beiträge: 1556
|
| Verfasst am: 25.04.2009, 10:43 Titel: |
|
|
| ralfkannenberg hat Folgendes geschrieben: | | Wenn diese also tatsächlich exponentiell anwachsen, so werden sie irgendwann einmal die Materie des gesamten Universums akkretiert haben [...] |
Hallo Ralf
Das möchte ich noch ein wenig ergänzen. Für einen Regelvorgang reicht es nicht einzig das potentiell vorhandene Futter zu betrachten. So würde ein Regelvorgang praktisch erst dann eintreten, wenn das ganze Universum gefuttert wurde. Man muss betrachten, ob und wieviel Futter tatsächlich in 'Fressreichweite' des BHs gelangt.
Zum Beispiel wenn ein BH schon die ganze Erde verschlungen hat, wird es nicht so weiter wachsen wie zuvor. Es befindet sich in einer stabilen Umlaufbahn um die Sonne und es kommt nicht mehr Materie an, wie auch so (Erde als nichtBH) jährlich auf die Erde fällt. Dadurch wird das Wachstum radikal verlangsamt.
Bei einem MiniBH verhält sich das ähnlich, denn die Abstandsverhältnisse zwischen MBH und den Materiebausteinen sind ähnlich wie im Sonnensystem. In dieser Microwelt steht es sogar noch schlechter für ein großes Wachstum, weil die Gravitation praktisch gar keine Rolle spielt. Allein elektromagnetischen Kräfte sind um endliche Größenordnungen stärker, als das bißchen Gravitation eines MBH. Ich wette darauf, das dort Rösslers elementarer Fehler liegt. Er geht von quasi von präatomistischen Materie aus. Es gibt keine Elementarbausteine, sondern die Materie ist kontinuierlich im Raum verteilt, beliebig zerteilbar. Wenn man ein größeres schwarzes Loch betrachtet, so mag das eine sehr gute Näherung sein. Bei MBHs ist ein solches Vorgehen jedoch sträflich.
Ein anderes Beispiel: Damit eine Bakterienkultur (die abschnittweise exponentiell wächst) reicht es nicht, das es irgendwo potentielles Futter gibt, sondern das Futter muss sich dort befinden, wo sich die Bakterien befinden.
mfg |
|
| Nach oben |
|
|
ralfkannenberg
Anmeldedatum: 22.02.2006
Beiträge: 4788
|
| Verfasst am: 25.04.2009, 11:27 Titel: |
|
|
| El Cattivo hat Folgendes geschrieben: | | Das möchte ich noch ein wenig ergänzen. Für einen Regelvorgang reicht es nicht einzig das potentiell vorhandene Futter zu betrachten. So würde ein Regelvorgang praktisch erst dann eintreten, wenn das ganze Universum gefuttert wurde. Man muss betrachten, ob und wieviel Futter tatsächlich in 'Fressreichweite' des BHs gelangt. |
Hallo El Cattivo,
das ist selbstverständlich richtig, was Du schreibst - ich hatte mich der Einfachheit halber mit einem 'worst case'-Szenario, also einer einfachen Abschätzung zur sicheren Seite hin, begnügt; schon damit kann man zeigen, dass die Akkretion und somit das Wachstum in endlicher Zeit zum erliegen kommt, und zwar sogar unabhängig davon, ob es exponentiell oder anders erfolgt.
Wenn man genauere Aussagen gewinnen möchte, so muss man natürlich wie Du das beschrieben hast weitere Randbedingungen beachten.
Im Übrigen werden diese verschiedenen Randbedingungen in der Sicherheitsanalyse von Giddings und Mangano berücksichtigt, auch wenn dies britikerseitig gerne "übersehen" wird.
Freundliche Grüsse, Ralf |
|
| Nach oben |
|
|
Orbit
Anmeldedatum: 29.09.2008
Beiträge: 1469
|
| Verfasst am: 25.04.2009, 11:39 Titel: |
|
|
| Zitat: | | Ich wette darauf, das dort Rösslers elementarer Fehler liegt. Er geht von quasi von präatomistischen Materie aus. Es gibt keine Elementarbausteine, sondern die Materie ist kontinuierlich im Raum verteilt, beliebig zerteilbar. |
El Cattivo
Das vermutete auch ich, als ich schrieb, er wolle seine Chaostheorie, welche für selbstorganisierte Makrosysteme gilt, 1to1 auf die Quantenwelt übertragen und somit die Quantentheorie neu erfinden. Das ist aber genau so unsinnig wie seine 'Ergänzung' zur RT.
Orbit |
|
| Nach oben |
|
|
richy
Anmeldedatum: 03.01.2007
Beiträge: 506
Wohnort: 76
|
| Verfasst am: 26.04.2009, 18:41 Titel: |
|
|
Hi Ralf
Vielen Dank, dass du meine Entschuldigung angenommen hast.
Vielleicht noch ein paar Gedanken zur Funktion y(x)=0, die ich im folgenden als "Nullfunktion" bezeichnen moechte.
Ich habe diese zunaechst intuitiv ueber den Grenzwert limes(a->0, y(x)=a) also als konstante nichtlineare Funktion betrachtet. Ebenso laesst sich der Grenzwert limes(a->0, y(x)=a*x) verwenden, der den linearen Charakter der Nullfunktion intuitiv erklaert.
So dass man beruhigt sein koennte.
Man kann weitere Grenzwerte konstruieren aus denen die Nullfunktion hervorgeht.
Wie zum Beispiel limes(a->0, y(x)=a*x^2) oder allgemein limes(a->0, y(x)=a*g(x))
| ralf hat Folgendes geschrieben: | | Die Nullfunktion ist (wie oben gezeigt und im Gegensatz zu Deiner Behauptung) trivialerweise linear ! |
Die mathematische Definition der Linearitaet ist mir bekannt und daher kann ich deinem Satz zustimmen. Aber es laesst sich ebenso zeigen, dass die Nullfunktion nichtlinear ist. Denn ich kann damit argumentieren, dass sie bezueglich der Linearitaetskriterien die selben Eigenschaften aufweist wie z.B. die quadratische nichtlineare Funktion y(x)=x^2 :
Das k fache Argument (Input) liefert einen k^2 fachen Funktionewert (Output) :
y(k*x)=0=k^2*0
Und schon diese nichtlineare Eigenschaft duefte eine lineare Funktion nicht erfuellen.
Das additive Kriterium laesst sich am einfachsten ueber
y(x)=0=limes(a->0,a*x^2) formulieren.
Ich meine daher, dass es sich anhand der Schreibweise y(x)=0 gar nicht entscheiden laesst ob die Nullfunktion linear oder nichtlinear ist. Sie erfuellt die Definition der Linearitaet, aber genausogut laesst sich die Funktion als Grenzwert darstellen, so dass sie die Definition der Linearitaet nicht erfuellt. Ohne Angabe des Grenzwertes auf der die Nullfunktion basiert macht eine Angabe zur Linearitaet damit doch eher wenig Sinn.
Es ist mir auch nicht so ganz einsichtig warum eine nichtlineare Funktion g(x) beim Grenzuebergang limes(a->0, y(x)=a*g(x)) linearisiert werden sollte.
Dies basiert letztendlich darauf weil ich pruefe ob die Funktion linear ist. Und nicht ob sie nichtliear ist
Darauf gruendete meine (selbstverstaendlich uebertriebene) Aufregung.
Viele Gruesse |
|
| Nach oben |
|
|
ralfkannenberg
Anmeldedatum: 22.02.2006
Beiträge: 4788
|
| Verfasst am: 27.04.2009, 09:13 Titel: |
|
|
| richy hat Folgendes geschrieben: | Vielleicht noch ein paar Gedanken zur Funktion y(x)=0, die ich im folgenden als "Nullfunktion" bezeichnen moechte.
Ich habe diese zunaechst intuitiv ueber den Grenzwert limes(a->0, y(x)=a) also als konstante nichtlineare Funktion betrachtet. Ebenso laesst sich der Grenzwert limes(a->0, y(x)=a*x) verwenden, der den linearen Charakter der Nullfunktion intuitiv erklaert. |
Hallo richy,
bitte beachte, dass Du dieselben identisch gleichen Überlegungen anstatt mit der Nullfunktion auch mit jeder beliebigen linearen Funktion anstellen kannst.
| richy hat Folgendes geschrieben: | | Man kann weitere Grenzwerte konstruieren aus denen die Nullfunktion hervorgeht. |
Insbesondere kann man also weitere Grenzwerte konstruieren, aus denen jede beliebige lineare Funktion hervorgeht.
| richy hat Folgendes geschrieben: | | Ich meine daher, dass es sich anhand der Schreibweise y(x)=0 gar nicht entscheiden laesst ob die Nullfunktion linear oder nichtlinear ist. Sie erfuellt die Definition der Linearitaet, aber genausogut laesst sich die Funktion als Grenzwert darstellen, so dass sie die Definition der Linearitaet nicht erfuellt. |
Somit gelangst Du zur gleichen Aussage für beliebige lineare Funktionen 
| richy hat Folgendes geschrieben: | | Ohne Angabe des Grenzwertes auf der die Nullfunktion basiert macht eine Angabe zur Linearitaet damit doch eher wenig Sinn. |
Gemäss dieser Argumentation würde ohne Angabe des Grenzwertes auf der die beliebige lineare Funktion basiert eine Angabe zur Linearitaet damit doch eher wenig Sinn machen.
| richy hat Folgendes geschrieben: | | Es ist mir auch nicht so ganz einsichtig warum eine nichtlineare Funktion g(x) beim Grenzuebergang limes(a->0, y(x)=a*g(x)) linearisiert werden sollte. |
Doch doch - genau das hast Du bewiesen: Es gibt nicht-lineare Funktionen, die man durch Grenzwertbildung "linearisieren" kann. Ich vermute, dass das sogar für jede nicht-lineare Funktion gilt, habe mir das aber nun im Detail nicht überlegt.
Freundliche Grüsse, Ralf |
|
| Nach oben |
|
|
zeitgenosse
Anmeldedatum: 21.06.2006
Beiträge: 1811
|
| Verfasst am: 27.04.2009, 10:10 Titel: |
|
|
Ursprünglich ging es um Rösslers Behauptung "Nichtlinear ist immer schneller". Im Kontext des Wachstumsprozesses stimmt diese Aussage.
Als Beispiel diene die logistische Funktion:
y = 1/(1 + exp(-t))
Verbindet man Anfangs- und Endpunkt des Graphen der obigen Funktion mit einer Geraden, erkennt man unschwer, dass die nichtlineare Funktion ihr Maximum wesentlich schneller erreicht. Am Schluss ist nur noch eine (unmerkliche) asymptotische Näherung vorhanden, welche in praxi nicht relevant ist.
Die logistische Funktion (Verhulstmodell) kommt der Realität natürlicher Wachstumsprozesse somit sehr nahe, weil irgendwann infolge der Kapazitätsgrenze der Ressourcen eine Sättigung eintritt. Man müsste sich diesen Punkt auch bei einem 'Black hole' ins Auge fassen. Wann kommt es dort eigentlich zur Sättigung? Wo liegt der Wendepunkt?
Unbegrenztes Wachstum ist in der Natur schlichtweg unmöglich. Somit stellt sich auch die Frage, ob es zu einem chaotischen Verhalten kommen könnte. In diesem Fall wäre der Lyapunov-Exponent positiv.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
|
Aragorn
Anmeldedatum: 23.06.2006
Beiträge: 1120
|
| Verfasst am: 27.04.2009, 11:35 Titel: |
|
|
Hier sieht man den "gigantischen Unterschied" der sich ergibt zwischen dem Kurvenverlauf der Funktionen y=0,2*x+0,5 und der immer ach so schnellen nichtlinearen Wachstumsfunktion y=1/(1-e^-x), im Intervall x=0 bis x=3:
Bei y=1 liegt das Maximum der immer und überall so "gigantisch schnell" anwachsenden e-Fkt.
Gruß Helmut |
|
| Nach oben |
|
|
zeitgenosse
Anmeldedatum: 21.06.2006
Beiträge: 1811
|
| Verfasst am: 27.04.2009, 12:38 Titel: |
|
|
| Aragorn hat Folgendes geschrieben: | | Bei y=1 liegt das Maximum der immer und überall so "gigantisch schnell" anwachsenden e-Fkt. |
Kein Kunststück - wenn du statt einem Plus ein Minus einträgst!
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
|
Aragorn
Anmeldedatum: 23.06.2006
Beiträge: 1120
|
| Verfasst am: 27.04.2009, 14:48 Titel: |
|
|
Ok, das habe ich im Text falsch hingeschrieben. Schau auf das Bild. Dort stehts korrekt. Dargestellt ist der Funktionsgraph
y=1/(1+e^-x) und
y=0,15*x+0,5.
Die 0,15 hat Excel bei der Beschriftung auf 0,2 gerundet.
Gruß Helmut |
|
| Nach oben |
|
|
El Cattivo
Anmeldedatum: 22.04.2007
Beiträge: 1556
|
| Verfasst am: 27.04.2009, 16:35 Titel: |
|
|
| zeitgenosse hat Folgendes geschrieben: | | Ursprünglich ging es um Rösslers Behauptung "Nichtlinear ist immer schneller". Im Kontext des Wachstumsprozesses stimmt diese Aussage. |
Ist diese Aussage ebenso falsch.
| zeitgenosse hat Folgendes geschrieben: | Als Beispiel diene die logistische Funktion:
y = 1/(1 + exp(-t))
|
Da bei der logistischen Funktion im physikalischen Kontext nur für t>0 interessant ist und y(0) dem Startwert entspricht. Also das, was man von vorne herein hat, was das auch immer sein mag. Eine lineare Funktion die schneller wächst:
f(t)=m*t+0,5 mit m>1
Du kannst noch ewig nichtlineare Wachstumsprozesse angeben. Ich finde immer ein lineares Wachstum, das schneller wächst. Einfach aus der Tatsache heraus, dass es in der Physik praktisch kein unendliches Wachstum gibt.
mfg |
|
| Nach oben |
|
|
zeitgenosse
Anmeldedatum: 21.06.2006
Beiträge: 1811
|
| Verfasst am: 27.04.2009, 19:31 Titel: |
|
|
| El Cattivo hat Folgendes geschrieben: | | Ich finde immer ein lineares Wachstum, das schneller wächst. |
Aber nicht im Kontext:
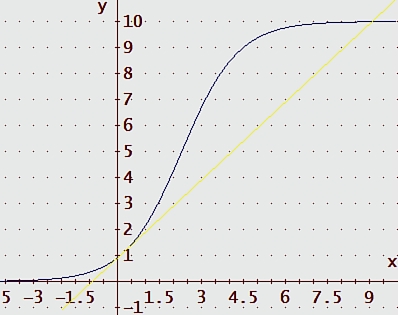
Hierzu sind Start- und Endpunkte der nichtlinearen Funktion durch eine Gerade zu verbinden. Alle anderen Geraden sind im Kontext nicht relevant. Nun ist offen ersichtlich, dass die logistische Funktion als erste in den Sättigungsbereich gelangt.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
|
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|
FAQ
Suchen
Mitgliederliste
Benutzergruppen
Registrieren
Profil
Einloggen, um private Nachrichten zu lesen
Login
