| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 23.11.2008, 01:37 Titel: Verfasst am: 23.11.2008, 01:37 Titel: |
 |
|
| zeitgenosse hat Folgendes geschrieben: |
Ein weiterer Aspekt der Tensorrechnung ist die Überschiebung. Dirschmid (Tensoren und Felder) schreibt dazu: "Die Produktbildung zweier Tensoren mit anschliessender Verjüngung nennt man Überschiebung." Die Überschiebung erniedrigt die Stufe des Produkttensors um zwei.
Ist es etwa dieser Sachverhalt, den Heim mit dem Matrizenspektrum angesprochen hat?
|
Hallo zeitgenosse,
ich bin beim Querlesen der Elementarstrukturen nochmal über dieses Thema "gestolpert" und habe dabei heraus gefunden, dass Heim die Begriffe hier durchaus korrekt bezeichnet. Die Verjüngung, bzw. Kontraktion von Tensoren bezeichnet Heim völlig richtig als MatrizenSPUR (leider mischt Heim die Begriffe Matrix und Tensor immer wieder, so dass Mathematiker hier natürlich regelmäßig Bauchschmerzen bekommen). Das Matrizenspektrum ist dagegen die Menge der Eigenwerte der Matrix/des Tensors. Das sind, wie Heim richtig beschreibt, auch die Diagonalelemente der Matrix nach einer Hauptachsentransformation (s.a. S. 69, ES Band 1).
Neulich ist mir auch klar geworden, was Heim mit der Bezeichnung (N)MOD(1)=0 meint. Er benutzt das recht oft und es bedeutet offensichtlich, dass N ganzzahlig sein soll  . Darauf muss man natürlich auch erst mal kommen. . Darauf muss man natürlich auch erst mal kommen.
Als Anregung: Man könnte als Nachbarthema eventuell noch das Thema Metronenrechnung anlegen. Auch dieses Thema ist eine enorme "Spielwiese" für eigene Überlegungen mit vielen Bezügen zur aktuellen Forschung. Allerdings fühle ich mich in dieser Thematik aktuell zu wenig zu Hause, als dass ich da einen geeigneten Aufhänger schreiben könnte.
Freundliche Grüße
Barney
Zuletzt bearbeitet von Barney am 03.01.2009, 13:18, insgesamt 2-mal bearbeitet |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 23.11.2008, 12:08 Titel: Verfasst am: 23.11.2008, 12:08 Titel: |
 |
|
| Barney hat Folgendes geschrieben: | | habe dabei heraus gefunden, dass Heim die Begriffe hier durchaus korrekt bezeichnet. Die Verjüngung, bzw. Kontraktion von Tensoren bezeichnet Heim völlig richtig als MatrizenSPUR (leider mischt Heim die Begriffe Matrix und Tensor immer wieder, so dass Mathematiker hier natürlich regelmäßig Bauchschmerzen bekommen). Das Matrizenspektrum ist dagegen die Menge der Eigenwerte der Matrix/des Tensors. Das sind, wie Heim richtig beschreibt, auch die Diagonalelemente der Matrix nach einer Hauptachsentransformation |
Gratuliere! Selbst habe ich nämlich auch gemerkt, dass das Matrizenspektrum unmöglich die Matrizenspur sein kann. Dass es die Eigenwerte sind, liegt für mich somit auf der Hand, insbesondere, wenn man Heims Überführung in den Mikrobereich und wieder zurück in den Makrobereich nachvollzieht (und wie ich bereits weiter oben sinngemäss beschrieb):
| Zitat: | | Übrig bleiben von den 64 Energiedichtespektren schliesslich 36 geometrisierte Energiestufen eines einheitlichen elementaren Materiefeldquants Mq. Diese werden - bedingt durch das Kovarianzprinzip - als Elemente eines 6-reihigen Energiedichte-Tensors verstanden [...] Aufgrund der tensoriellen Gesetzmässigkeiten verschwinden nochmals 12 Eigenwerte, so dass 24 unabhängige Komponenten übrigbleiben. |
Immerhin haben wir durch die eingeschlagene dialektische Vorgehensweise zumindest einen wichtigen Grundbegriff (Matrizenspektrum) deutlich aus dem der Nacht folgenden Morgennebel herausgeschält, so dass das Licht des Tages bereits vereinzelt aus dem Gewölk hervorbricht!
Was die Metronenrechnung anbelangt, müsste man sich zuerst etwas in den Differenzenbegriff (z.B. Sauer, Differenzengeometrie) einlesen, bevor man sich dem Heimschen Selektorkalkül nähert. Während bei Sauer aber eine rein mathematische Motivation zugrunde liegt, ist es bei Heim ein physikalisch-geometrischer Ansatz, der zu völlig neuen Methoden führt.
p.s.
Wieder einmal mehr kristallisiert sich für mich heraus, dass Heim die Dinge durchaus richtig ansetzt, allfällige Unstimmigkeiten hingegen oft durch seine zuweilen eigenwillige Notation und seine offensichtliche Vorliebe zum Überspringen von Zwischenschritten hervorgerufen werden (was dann die ungefestigten Kritiker zu einem Verriss der Heimschen Theorie motiviert ohne dass sie die Kernthesen überhaupt auch nur ansatzweise verstanden haben). 
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 10.02.2009, 00:12 Titel: Verfasst am: 10.02.2009, 00:12 Titel: |
 |
|
nach längerer Pause möchte ich mal zusammenfassen:
In den Elementarstrukturen Band 1 werden bei grober Betrachtung zwei scheinbar alternative Gravitationstheorien vorgeschlagen:
1.) $\partial_{\alpha }G^{\alpha \beta} = j^{\beta}$ (s.o.)
2.) Die Feldgleichungen der ART, erweitert auf sechs Dimensionen.
Ich frage mich momentan, ob es nicht möglich ist aus Punkt 2 Punkt 1 abzuleiten. Also in Analogie zur Linearisierung der Feldgleichungen der ART unter der Nebenbedingung, dass die gesuchte Metrik nur wenig von der Minkowskimetrik abweicht.
Über die Bedingungen einer solchen Ableitung bin ich mir noch nicht wirklich im Klaren, aber ich denke dass diese Frage prinzipiell gut zu klären sein sollte. Es wäre deswegen interessant, wenn dazu noch ein weiterer Gedankenaustausch stattfinden könnte. |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 10.02.2009, 01:58 Titel: Verfasst am: 10.02.2009, 01:58 Titel: |
 |
|
Servus Barney!
In aller Kürze, was ich bereits andernorts angesprochen hatte:
Inzwischen haben einige in Heims korrigiertem Gravitationsgesetz einen gravierenden Fehler gefunden. Eliminiert man diesen, stimmt das Gesetz und es lässt sich auch ein Bezug zur ART herstellen.
Nach Heim ist:
phi = - G*M(r)/r
M(r) ist die "gravitative Masse", d.h. felderzeugende Masse + Feldmasse.
Doch dies wäre nicht kompatibel mit der Poissongleichung (welche doch empirisch bestätigt ist):
Laplace phi = 4pi*G*rho ; mit rho Massendichte
Korrekt hingegen - d.h. kompatibel mit Poisson - wäre, um Heims Ansatz beizubehalten:
Nabla phi = dphi/dr = G*M(r)/r^2
Heims Dgl für die Gravitation lautet:
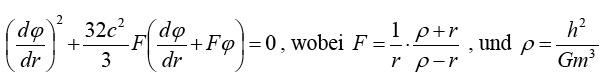
Als eine denkbare Lösung bietet sich an:
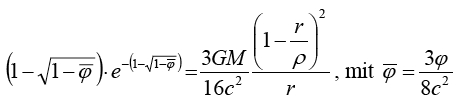
Ausgehend von:
phi = - G*M(r)/r
erhält man für M(r) die Lösung:
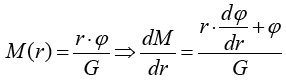
In der ART gilt für die Dichte der Feldmasse:
rho + 3p/c^2
(mit rho Massendichte und p Druckkomponente des Feldes)
Im Weiteren gilt:
rho = - (nabla phi)^2/8pi*G*c^2 ; phi ist das Gravitationspotential
und p = rh0*c^2
somit für die Feldmassendichte (die in der ART auch vorkommt):
rho_feld = -(Nabla phi)^2/2pi*G*c^2
Das Minuszeichen bedeutet, dass die Feldmassendichte die Gesamtmasse eines Körpers verringert, wenn man sich aus dem Mittelpunkt des Körpers herausbewegt. Soweit ist das Standardtheorie (wie man in jedem besseren Lehrbuch der ART selbst nachlesen kann).
Letztlich erhalten wir auf diesem Wege:
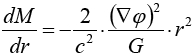
Substituiert man nun die Heimsche Lösung für M(r) in die obige Gleichung, bekommt man:
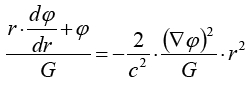
und erhält für die Feldbeschleunigung die korrekte Lösung:
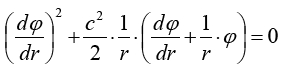
Diese unterscheidet sich nur durch den Faktor (1/2) anstatt (32/3) von der Heimschen Gleichung! Offensichtlich hat Heim die Feldmasse falsch interpretiert. Die Hauptarbeit für diese nötige Korrektur hat Börje Månsson (ein schwedischer Physiklehrer) geleistet.
Dazu siehe:
http://home.comcast.net/~djimgraham/INDEX.HTML
Die bereinigte Lösung (ohne Feldmasse) kann als eine Lösung der Einsteinschen Feldgleichungen betrachtet werden. Damit ist evident, dass sich der Feldverlauf erheblich von dem Graphen in der Skizze von Posdzech unterscheidet.
Verlauf des Feldes nach Heim:
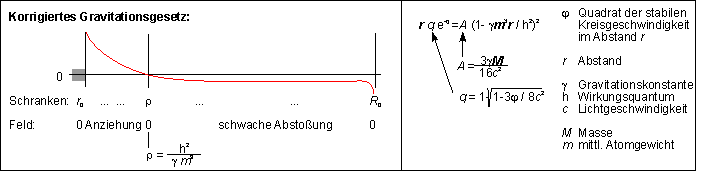
Heims Formel
rh0 = h^2/(G*m^3)
- welche die Atommassen der Gravitationsquelle mit der Stärke der durch sie erzeugten Gravitation verbindet (was zur Folge hat, dass sie sich im Unterschiede zu Newtons Theorie verringert) - kann dann so interpretiert werden, dass es die gewöhnlichen Massen (baryonische Materie) im Universum sind, die Dark energy generieren. Die kosmologische Konstante wäre aus dieser Sicht der Beitrag sämtlicher Massen im optischen Universum zur Quintessenz. Es resultiert gewissermassen eine Abstossung des Raumes selbst, was sich für den Beobachter als Expansion äussert. Die Massen ziehen an, der Raum dehnt sich aus. Das hat zur Folge, dass für r > rho eine Abstossung (Repulsion) herauskommt, wie das auch Heim in seinem korrigierten Gravitationsgesetz beabsichtigte. Das alles ist natürlich nur dann von Relevanz, wenn Heims obige Distanzformel sich als richtig erweist.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 10.02.2009, 22:23 Titel: Verfasst am: 10.02.2009, 22:23 Titel: |
 |
|
Hallo zeitgenosse,
dein voriger Beitrag ist wirklich sehr interessant und ich gebe es gerne zu: ich verstehe die Ableitungen von B. Mansson nur ansatzweise.
Die Ergebnisse sind allerdings sehr ermutigend. Denn er bekommt als Lösung der korrigierten Heimschen DGL tatsächlich eine modifizierte Schwarzschildmetrik! Besonders gut gefällt mir an der ganzen Thematik natürlich auch die Möglichkeit, auf sehr natürliche Weise eine Erklärung für die dunkle Materie/Energie via Feldmasse zu geben. Je länger ich darüber nachdenke, desto mehr festigt sich bei mir die Überzeugung, dass der Weg doch in diese Richtung gehen MUSS. Die völlig erfolglose Suche nach neuartigen Elementarteilchen zur Erklärung der dunklen Materie verkommt doch von Tag zu Tag mehr und mehr zu einer gigantischen Farce. Man entschuldige mir bitte diesen Ausdruck, aber ich finde da momentan einfach kein besseres Wort dafür.
Was mir an den ganzen Potentialbetrachtungen leider auch noch völlig unklar ist, ist die Frage, wie man von einem kugelsymmetrischen Potential $\varphi (r)$ zu einer Periheldrehung auf geodätischen Bahnen kommen kann (also z.B. Periheldrehung des Merkur). Bei der ART kann man sich das über den Gangunterschied der Eigenzeit sehr leicht erklären, aber wie soll das hier bei der Heimschen Theorie funktionieren?
Gruß
Barney |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 11.02.2009, 11:07 Titel: Verfasst am: 11.02.2009, 11:07 Titel: |
 |
|
| Barney hat Folgendes geschrieben: | | Was mir an den ganzen Potentialbetrachtungen leider auch noch völlig unklar ist, ist die Frage, wie man von einem kugelsymmetrischen Potential... |
Einstein hat bei seiner Herleitung des Merkurperihels auch ein kugelsymmetrisches Zentralfeld verwendet:
∆φ = 6GMπ/(a(1 - ε²)c²)
(a grosse Halbachse; ε Exzentrizität)
∆φ ist die (zusätzliche) Drehung der Apsidenlinie im Bogenmass.
Die ART sagt ein säkulares Perihel von 43.03 Bogensekunden voraus, was sehr gut mit der Beobachtung harmoniert. Der Merkur hat dann bereits 415 Umdrehungen hinter sich.
Zu einem ähnlichen Betrag des Merkurperihels ist vor Einstein bereits Gerber gelangt (Über die räumliche und zeitliche Ausbreitung der Gravitation, Zeitschr. f. Math. u. Phys. 1898). Dies gelang ihm unter der Voraussetzung einer endlichen Wirkungsgeschwindigkeit der Gravitation, die Gerber gleich der Lichtgeschwindigkeit annahm. Gerber war ein kluger und in der Mathematik bewanderter Gelehrter. Sein Artikel fand jedoch kaum Beachtung.
Gerbers Herleitung möchte ich dem Leser ersparen, das Ergebnis hingegen soll nicht vorenthalten werden:
c² = 6πμ/(a(1 - ε²)ψ)
Der Gerberschen Hypothese vorausgegangen waren die Bemühungen von Weber, Riemann und Levy, die mit einem postnewtonschen Ansatz arbeiteten, bei dem das Webersche Grundgesetz eine entscheidende Funktion ausübt. Diese mussten sich gegenüber der Laplace'schen Kritik behaupten, weil Laplace gezeigt hatte, dass die Gravitationsausbreitung entweder instantan oder sehr viel schneller als mit Lichtgeschwindigkeit erfolgen müsse. Laplace's These erwies sich später als falsch (und belegt, dass sich auch grosse Himmelsmechaniker ab und zu irren). Problematisch bei einer endlichen Wirkungsgeschwindigkeit blieb aber die dann zu erwartende Aberration.
Lorentz (1902) versuchte sich an einem auf elektrischen Differenzkräften beruhenden Erklärungsansatz, erhielt aber im Unterschied zu Gerber einen zu geringen Wert. Immerhin kam Lorentz zum richtigen Schluss: ...was bis jetzt gesagt wurde reicht aus um zu zeigen, dass die Gravitation auf Aktionen zurückgeführt werden kann, welche sich nicht schneller als mit Lichtgeschwindigkeit ausbreiten...
Zwei Jahre später vermochte Poincaré zu begründen, weshalb im Rahmen der Lorentzschen Äthertheorie kein Gruppensignal schneller als die Lichtgeschwindigkeit ist. Ansonsten würde u.a. auch die Synchronisationsvorschrift für Lichtsignale (und damit auch die von Lorentz eingeführte Ortszeit) hinfällig.
Eine physikalisch konsistente Herleitung des Merkurperihels gelang - wie einleitend angetönt - aber erst Einstein (1915), wobei dieser mit der ganzen Rechnerei ordentlich Mühe bekundete und - als das bangungsvolle Erwarten einer freudigen Gewissheit wich - vor Aufregung nicht mehr schlafen konnte. Vorausgegangen waren Jahre des Zweifels und teilweise falscher Berechnungen. In einem Brief an Arnold Sommerfeld schrieb Einstein: Denk Dir meine Freude ... , dass die Gleichungen die Perihel-Bewegung des Merkur richtig liefern. Und an den Freund Paul Ehrenfest: Ich war einige Tage fassungslos vor freudiger Erregung.
Ja, es war in Summe eine durchaus reife Leistung, die eines Genius würdig ist!
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 11.02.2009, 18:29 Titel: Verfasst am: 11.02.2009, 18:29 Titel: |
 |
|
| zeitgenosse hat Folgendes geschrieben: |
Einstein hat bei seiner Herleitung des Merkurperihels auch ein kugelsymmetrisches Zentralfeld verwendet:
|
Hallo zeitgenosse
kennst du dazu eventuell öffentlich einsehbare Quellen. Mir ist dieser Satz ebenfalls aus den Einstein-Biografien bekannt, aber die Herleitung selbst kenne ich - peinlicherweise (?) - nicht. In den Lehrbüchern zur ART findet man normalerweise immer nur die Herleitung aus der Schwarzschildmetrik.
Gruß
Barney |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 12.02.2009, 01:46 Titel: Verfasst am: 12.02.2009, 01:46 Titel: |
 |
|
| Barney hat Folgendes geschrieben: | | kennst du dazu eventuell öffentlich einsehbare Quellen. |
Für einmal muss ich dich enttäuschen.
Es finden sich in der Tat nicht viele Belege zur Einsteinschen Herleitung der Perihelverschiebung. Wenn ich offen sein darf: Selbst habe ich auch keine zur Hand. Reichenbach, sonst ein emsiger Befürworter der Relativistischen Physik, zweifelt in seinem Buch "Die philosophische Bedeutung der Relativitätstheorie" sogar an der diesbezüglichen Relevanz. Auch bei Pauli finden wir keine weiterführenden Einsichten.
Die Periheldrehung hat Einstein bereits im Rahmen seiner Entwurftheorie (1913) beschäftigt, wo ihm nebst Grossmann auch Freund Besso zur Seite stand. Im Oktober 1915 lieferte Einstein aber einen falschen Wert, im November desselben Jahres (nach Hilberts Veröffentlichung der Feldleichungen) folgte eine korrigierte Version:
"Erklärung der Perihelbewegung des Merkur aus der Allgemeinen Relativitätstheorie" (Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften, Berlin).
Hilbert gratulierte Einstein dazu, dass ihm die Lösung des Problems so schnell geglückt sei. Dies gelang Einstein (nach Angaben seiner Biografen), weil er auf Rechnungen zurückgriff, die er bereits 1913/14 mit Besso durchgeführt hatte! Man wird trotzdem den Eindruck nicht los, dass gehörig nachgebessert wurde.
Am benutzten Calculus wird prinzipiell nicht gezweifelt. Es wird eine Näherungsrechnung gewesen sein.
Weil die Feldgleichungen der Gravitation von höherer Ordnung sind, tritt im zentralsymmetrischen Problem neben der Masse noch eine zweite (willkürliche) Integrationskonstante auf, wobei - wie Pauli zeigte - nur für eine spezielle Wahl dieser Integrationskonstanten die Einsteinsche Lösung für die Periheldrehung resultiert.
Gemäss der ART weicht das Gravitationspotential in erster Näherung um
δV(r) = β/r²
vom Kepler-Gesetz ab. Die Addition einer kleinen Grösse δV(r) zum Kepler-Potential hat somit eine Periheldrehung δφ zur Folge. Die Newtonschen Bewegungsgleichungen müssen deshalb korrigiert werden.
Einwände von gewisser Seite, dass die Restverschiebung von 43" auf die Abplattung der Sonne zurückzuführen sei, greifen nach Ansicht der Fachwelt viel zu wenig. Fliessbach, Allg. Relativitätstheorie, widmet der Angelegenheit ein ganzes Kapitel. Problematisch erscheint vielmehr, dass die theoretischen Werte mit zunehmendem Sonnenabstand - somit für die übrigen Planeten - stärker von den empirischen Werten abweichen, als dies beim Merkur der Fall ist - prozentual gesehen.
Gr. zg
_________________
Make everything as simple as possible, but not simpler!
Zuletzt bearbeitet von zeitgenosse am 12.02.2009, 02:42, insgesamt 3-mal bearbeitet |
|
| Nach oben |
|
 |
pauli
Anmeldedatum: 13.06.2007
Beiträge: 1551
|
 Verfasst am: 12.02.2009, 02:32 Titel: Verfasst am: 12.02.2009, 02:32 Titel: |
 |
|
Also da bin ich jetzt etwas überrascht, wird doch die Merkur-Periheldrehung in zig Zeitschriften und Büchern als ein klarer Beweis pro ART aufgeführt! In den letzten ca. 90 Jahren wird das doch wohl irgendjemand nachgerechnet haben, und wenn nur zum Spaß? Oder ist es soo schwierig dass es ein Einzelner etwa garnicht kann?  |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 12.02.2009, 10:17 Titel: Verfasst am: 12.02.2009, 10:17 Titel: |
 |
|
Hallo pauli,
Die Berechnung der Periheldrehung des Merkur ist natürlich kein Problem und in jedem Lehrbuch zur ART nachzulesen. Es geht aktuell jedoch um ein ganz anderes Thema. |
|
| Nach oben |
|
 |
zeitgenosse

Anmeldedatum: 21.06.2006
Beiträge: 1811
|
 Verfasst am: 12.02.2009, 10:47 Titel: Verfasst am: 12.02.2009, 10:47 Titel: |
 |
|
Dr. Christoph Pöppe schreibt in "Der Golem der Forschung. Wie unsere Wissenschaft die Natur erfindet" die folgenschweren Sätze:
| Zitat: | Eine der bedeutendsten Arbeiten Albert Einsteins enthält an einer entscheidenden Stelle einen Fehler. Es geht um die Perihelpräzession des Merkur...
Einstein berechnet in seiner Veröffentlichung [...] in einer langen Herleitung die Geschwindigkeit dieser Präzession; dabei ist ein Integral falsch berechnet. Schulkenntnisse in Integralrechnung und eine übliche Formelsammlung reichen aus, das zu bestätigen.
Erschienen in 'Spektrum der Wissenschaft' (5/2000) |
Selbstkritisch bemerkte Einstein (1916) in einem Brief an Lorentz:
| Zitat: | | Die Serie meiner Gravitationsarbeiten ist eine Kette von Irrwegen, die aber doch allmählich dem Ziele näher führten. Daher sind nun endlich die Grundformeln gut, aber die Ableitungen abscheulich; dieser Mangel muss noch behoben werden... |
Ob etwa das der Grund dafür ist, dass Einsteins eigene Herleitung zur Periheldrehung aus der öffentlichen Literatur so gut wie verschwunden ist? Na ja, in den 'The Collected Papers of Albert Einstein' (Volume 6) wird man vermutlich fündig.
Born schrieb am 23. November 1915 an Hilbert:
| Zitat: | | ...Von Einstein und Freundlich hörte ich, dass Sie jetzt die Gravitation in Ordnung gebracht haben; auch konnte ich einen kurzen Auszug Ihres Vortrags in der mathematischen Gesellschaf einsehen [...] Einstein selber sagt, er habe das Problem ebenfalls gelöst, doch scheint mir seine Betrachtung (die ich nur aus Gesprächen kenne) ein Spezialfall der Ihrigen. Jedenfalls ist es ihm gelungen, die Anomalien der Planetenbahnen numerisch richtig aus seinen Formeln abzuleiten... |
Dass Einstein gelegentlich ihm unangenehme Vorarbeiten verschwieg, erkennt man unschwer auch in seiner kosmologischen Arbeit von 1917, wo er Schwarzschild's Beitrag zum zentralsymmetrischen Gravitationsfeld gänzlich unerwähnt lässt.
Zum Thema siehe:
H. Goenner, "Einstein in Berlin" (C.H. Beck)
p.s.
Mir geht's gewiss nicht um Polemik, sondern einfach nur um die Wahrheit.
Gr. zg
_________________
Make everything as simple as possible, but not simpler! |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 12.02.2009, 11:24 Titel: Verfasst am: 12.02.2009, 11:24 Titel: |
 |
|
| zeitgenosse hat Folgendes geschrieben: |
p.s.
Mir geht's gewiss nicht um Polemik, sondern einfach nur um die Wahrheit.
|
Hallo zg,
es muss einmal gesagt werden: Ich kenne sonst niemanden, der gerade in der Geschichte der Physik so belesen ist. Mein Anerkennung dafür ist Dir deswegen gewiss.
Freundliche Grüße
Barney
Zuletzt bearbeitet von Barney am 20.02.2009, 02:38, insgesamt 3-mal bearbeitet |
|
| Nach oben |
|
 |
Erik
Anmeldedatum: 28.03.2006
Beiträge: 565
|
 Verfasst am: 12.02.2009, 13:51 Titel: Verfasst am: 12.02.2009, 13:51 Titel: |
 |
|
| Barney hat Folgendes geschrieben: |
Die Berechnung der Periheldrehung des Merkur ist natürlich kein Problem und in jedem Lehrbuch zur ART nachzulesen. Es geht aktuell jedoch um ein ganz anderes Thema.
|
Um welches denn eigentlich? Zeitartige Geodäten in der Schwarzschild-Metrik sind Bahnkurven in einem
zentralsymmetrischen Potential. Dieses weicht von dem effektiven Kepler Potential, entgegen
zgs Behauptung nicht um einen Term ~1/r^2, sondern um einen Term ~1/r^3 ab.
| zeitgenosse hat Folgendes geschrieben: |
Weil die Feldgleichungen der Gravitation von höherer Ordnung sind, tritt im
zentralsymmetrischen Problem neben der Masse noch eine zweite (willkürliche)
Integrationskonstante auf, wobei - wie Pauli zeigte - nur für eine spezielle Wahl dieser
Integrationskonstanten die Einsteinsche Lösung für die Periheldrehung resultiert.
|
Was zeigte Pauli? Zitat, bitte. Alle zentralsymmetrischen Lösungen der Feldgleichungen
sind im Vakuum mit der Schwarzschildlösung identisch (Birkhoff-Theorem) und
die hat bekanntlich nur eine freie Konstante. Und in der Schwarzschildmetrik ergibt sich
der korrekte Wert für die Perihelverschiebung.
| zeitgenosse hat Folgendes geschrieben: |
Mir geht's gewiss nicht um Polemik, sondern einfach nur um die Wahrheit.
|
Mir drängt sich leider immernoch der Eindruck auf, dir geht es in erster Linie um die
Formulierung gut klingender Aussagen, die modernen wissenschaftlichen Jargon imitieren
und weniger um den Inhalt.
Wenn du wirklich wüßtest wovon du sprichst und an Klärung interessiert wärest, würdest
du kaum so nonchalant von einer "Dichte der Feldmasse" und einer "Druckkomponente des Feldes",
die es im Rahmen der ART geben soll, gesprochen haben, wie in einem Beitrag weiter oben.
Weißt du wie die lokalen Energie- und Impulsdichten des Gravitationsfeldes in der ART aussehen? |
|
| Nach oben |
|
 |
ralfkannenberg
Anmeldedatum: 22.02.2006
Beiträge: 4788
|
 Verfasst am: 12.02.2009, 14:58 Titel: Verfasst am: 12.02.2009, 14:58 Titel: |
 |
|
| zeitgenosse hat Folgendes geschrieben: | | Zu einem ähnlichen Betrag des Merkurperihels ist vor Einstein bereits Gerber gelangt (Über die räumliche und zeitliche Ausbreitung der Gravitation, Zeitschr. f. Math. u. Phys. 1898). |
Hallo zeitgenosse,
beachte bitte, dass Gerber von willkürlichen Parametern ausgeht und obendrein mit dem Gerber-Potential die Lichtablenkung am Sonnenrand eine andere wäre.
Es gibt dazu folgende Quelle: Roseveare, N. T.: Mercury's perihelion : from Leverrier to Einstein. Oxford 1982. 208 S.
Freundliche Grüsse, Ralf |
|
| Nach oben |
|
 |
Barney
Anmeldedatum: 19.10.2008
Beiträge: 1538
|
 Verfasst am: 12.02.2009, 20:56 Titel: Verfasst am: 12.02.2009, 20:56 Titel: |
 |
|
| Erik hat Folgendes geschrieben: |
Um welches denn eigentlich?
|
mich beschäftigt in diesem Zusammenhang ein mathematisches Problem: Ist es prinzipiell möglich in einem Newtonschen Intertialsystem mit einem kugelsymmetrischen Gravitationspotential zu einer Periheldrehung zu gelangen. Ich vermute nämlich, dass es da einen mathematischen Beweis geben könnte, dass das nicht möglich ist.
Noch einmal zusammengefaßt: Man nehme ein Newtonsches Inertialsystem mit euklidischer Metrik, eine absolute Zeitdefinition, die für alle Raumpunkte gilt, das Trägheitsgesetz F = m*a und ein beliebiges, nicht weiter festgelegtes, aber kugelsymmetrisches Zentralpotential phi(r). Kann man unter diesen Bedingungen Keplersche Bahnen (zumindest in guter Näherung) mit Periheldrehung ableiten? |
|
| Nach oben |
|
 |
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|