| Vorheriges Thema anzeigen :: Nächstes Thema anzeigen |
| Autor |
Nachricht |
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
 Verfasst am: 15.09.2008, 16:19 Titel: |
 |
|
@Chlorobium
Danke, das hatte ich auch schon entdeckt. Da haben wir auch wieder den riesigen Physiker.
@Aragorn
Wenn ich einem Trugschluß erliege, dann dem, daß ich fest davon ausgegangen bin, es müsse über eine ortsabhängige Funktion integriert werden.
Ein Lichtstrahl aus dem Sternbild Stier bewegt sich (aus ca. 44pc Entfernung) quasi radial auf die Sonne zu (die Sonne erscheint den Hyaden unter einem Öffnungwinkel ~1e-9 rad) um sie dann "flüchtig" zu tangieren. In Anwesenheit des Potentials der Sonne. Kann ich tangentiale und radiale Geschwindigkeit (in Richtung Beobachter) "einfach so" gleichsetzen? Oder werden diese Größen in unmittelbarer ~Nähe der Sonne korrekt 'abgehandelt', um später linear in Erscheinung zu treten? Da muß ich versuchen, eine gute Quelle zu finden. Da ich aus der nichtlinearen Thermodynamik komme, muß ich vielleicht meinen Blickwinkel anpassen.
P.S.:
Da die Sonne selbst tangentiale Lichstrahlen (in Bezug der Verbindunglinie Sonne-Mond-Erde bei Sonnenfinsternis) emittiert, könne diese 'Eigentangenten' die Funktion Tangierender von anderen Sternen übernehmen. Nimmt man also an, die Sonne erscheine daher qua selbst um einen Winkel von 2*1.75'' vergrößert?
gruß h |
|
| Nach oben |
|
 |
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 15.09.2008, 16:45 Titel: |
|
|
Hallo hamlet,
| hamlet hat Folgendes geschrieben: | | Kann ich tangentiale und radiale Geschwindigkeit (in Richtung Beobachter) "einfach so" gleichsetzen? |
nein, damit hat das nichts zu tun. Die ART sagt schlicht, dass eine ebene Lichtwelle, die Tangential an der Sonnenkannte einläuft, um 1.75" zum Zentrum abgelenkt wird. Unabhängig davon, woher diese Welle kommt und wohin sie geht. Die von dir zitierte Zeichnung wählt einfach die beiden Lichtstrahlen aus, die zufällig ins Auge des Riesenwissenschaftlers fallen. Ein anderer Beobachter sieht natürlich andere Strahlen am Sonnenrand passieren.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 15.09.2008, 17:56 Titel: |
|
|
Hallo Joachim,
Du schreibst:
| Zitat: | | Die ART sagt schlicht, dass eine ebene Lichtwelle, die Tangential an der Sonnenkante einläuft, um 1.75" zum Zentrum abgelenkt wird. |
Was passiert (im Verhältinis tangential zu radial) davor und was dahinter (deshalb mein Hinweis auf die große Entfernung zum Sternbild Stier)? Ist die Situation absolut symmetrisch? (Ich denke, sie ist es nicht, allein wegen f(Annäherung -> blau) != f(Entfernung -> rot)).
Oder ist dieser ausgezeichnete Moment des Tangierens die "ganze Physik" dahinter?
Ich will damit nicht meckern, eher gedenke ich, die Herleitung zur Berechnung der Geodäten zu begreifen. Wahrscheinlich steckt da das Detail drin.
gruß h |
|
| Nach oben |
|
|
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 15.09.2008, 18:11 Titel: |
|
|
Hallo hamlet,
| hamlet hat Folgendes geschrieben: |
Was passiert (im Verhältinis tangential zu radial) davor und was dahinter (deshalb mein Hinweis auf die große Entfernung zum Sternbild Stier)? Ist die Situation absolut symmetrisch? (Ich denke, sie ist es nicht, allein wegen f(Annäherung -> blau) != f(Entfernung -> rot)).
|
Man betrachtet einfach eine einlaufende ebene Welle und berechnet, wie sich die Wellenfront beim durchlaufen des Gravitationsfeldes verformt. Ganz weit außen passiert gar nichts und je näher die Wellenfront dem Massenzentrum kommt, desto mehr bleibt sie gegenüber einer (hypothethischen) undeformierten Welle zurück. Weit genug hinter dem Massenzentrum hat man dann keine Ebene Wellenfront mehr, sondern eine mit einer "Delle" im Zentrum. Ein Lichtstrahl ist jetzt eine Linie, die zu jeder Wellenfront, die sie passiert, orthogonal ist. Solch eine Linie wird um so mehr von der Geraden abgelenkt, je näher sie dem Zentrum kommt. Ein Lichtstrahl, der die Sonne gerade streift hat im Fernfeld eine Ablenkung von 1,75" erfahren.
Es ist also nicht symmetrisch: Die einlaufende Welle wird eben angenommen (weit entfernte Lichtquelle) und die auslaufende Welle ist deformiert.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 15.09.2008, 19:04 Titel: |
|
|
Hallo Joachim,
das leuchtet zunächst ein:
| Zitat: | | Man betrachtet einfach eine einlaufende ebene Welle und berechnet, wie sich die Wellenfront beim durchlaufen des Gravitationsfeldes verformt. |
Wie gefährlich das 'einfach' ist, wirft dann folgende Betrachtung auf:
| Zitat: | | Ganz weit außen passiert gar nichts und je näher die Wellenfront dem Massenzentrum kommt, desto mehr bleibt sie gegenüber einer (hypothethischen) undeformierten Welle zurück. Weit genug hinter dem Massenzentrum hat man dann keine Ebene Wellenfront mehr, sondern eine mit einer "Delle" im Zentrum. |
(P.S.: Erst ab dem Massenzentrum bleibt sie zurück?)
Denn äquivalent betrachtet, ohne spitzfindig sein zu wollen:
Fordert diese Aussage nicht dazu heraus zu postulieren, daß die 'ebene' Welle im Moment des ersten Kontakts mit der Sonnenoberfläche, d.h. auf dem 'Hinweg', ebenfalls eine "Delle" im Zentrum hat, und weil es sich um den 'Hinweg' handelt, diese Delle eine "Beule" sei?. Weiterhin es sich wenn, dann bei dieser Beule um einen radialen Effekt handelt?
Und wie weit ist 'weit genug' (Entfernungsabhängigkeit)? Was ja genau die Eingangsfrage war.
gruß hamlet |
|
| Nach oben |
|
|
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 15.09.2008, 19:17 Titel: |
|
|
Hi Hamlet,
| hamlet hat Folgendes geschrieben: |
(P.S.: Erst ab dem Massenzentrum bleibt sie zurück?)
|
Nein, auch schon vorher. Wie weit die Wellenfront zurückbleibt, hängt vom potential ab. das Potential klingt mit 1/r nach außen ab. Je tiefer eine Welle im Potential ist, desto langsamer breitet sie sich im Vergleich zu einer ungestörten Welle aus.
| hamlet hat Folgendes geschrieben: |
Fordert diese Aussage nicht dazu heraus zu postulieren, daß die 'ebene' Welle im Moment des ersten Kontakts mit der Sonnenoberfläche, d.h. auf dem 'Hinweg', ebenfalls eine "Delle" im Zentrum hat, und weil es sich um den 'Hinweg' handelt, diese Delle eine "Beule" sei?.
|
Nein, auch schon bei der Annäherung ist der Teil der Welle, der dem Massenzentrum näher ist, langsamer als es ohne Masse der Fall wäre. Die Delle beginnt sich schon bei der Annäherung der Welle auszubilden.
| Zitat: | | Und wie weit ist 'weit genug' (Entfernungsabhängigkeit)? Was ja genau die Eingangsfrage war. |
Das hängt von der gewünschten Genauigkeit des Ergebnisses ab. Die Quelle sollte so weit entfernt sein, dass bei ihr die von der Sonne ausgehende Gravitation nicht mehr messbar ist. Das ist für alle Sterne der Fall.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 15.09.2008, 19:47 Titel: |
|
|
Das ist, wenn es richtig ist, wirklich delikat:
| Zitat: | | Auch schon bei der Annäherung ist der Teil der Welle, der dem Massenzentrum näher ist, langsamer als es ohne Masse der Fall wäre. Die Delle beginnt sich schon bei der Annäherung der Welle auszubilden. |
Das bedeutet, daß das tangentiale Ereignis diesbezüglich ohne Vorzeichenwechsel auskommt, nicht wahr? Ob relative Annäherung oder Entfernung spielt keine Rolle. Aber ein 1/r-Gesetzt kennt doch auch in diesem Fall sicher ein f(dr)? - ob sich etwas annähert oder entfernt macht doch einen wichtigen (nicht zuletzt relativen) Unterschied (?).
gruß h |
|
| Nach oben |
|
|
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 15.09.2008, 19:59 Titel: |
|
|
Hallo Hamlet,
ich sehe wirklich nicht, was daran Delikat ist. Man erkennt es doch schon auf dem von dir verlinkten Bild dieser Seite.
Hier nochmal das Bild:
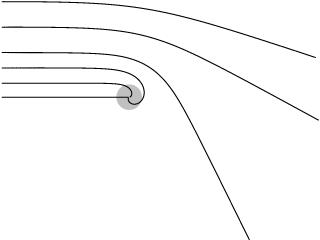
Die Krümmung der im unendlichen parallelen Strahlen wird um so stärker, je näher sie dem Ereignishorizont sind. Am punkt der größten Annäherung ist die Krümmung am stärksten und danach nimmt sie wieder ab. Sie ändert aber nirgends das Vorzeichen. Die Strahlen sind überall zur Masse hin gekrümmt. Symmetrisch ist das ganze bezüglich Zeitumkehr und bezüglich Rotation. Das heißt, jede Linie kann von einem Lichtstrahl in beide Richtungen durchlaufen werden und das parallele Strahlenbündel kann aus einer beliebigen Richtung kommen.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 15.09.2008, 20:28 Titel: |
|
|
Hallo Joachim,
delikat erschien mir eine Verletzung der Invarianz gegenüber Spiegelungen, ich dachte dabei, ggf. falsch herum, an das Noether-Theorem. Du hast auf die Symmetrie bezüglich der (lokalen) Zeitumkehr hingewiesen. Da muß ich drüber nachdenken.
gruß h |
|
| Nach oben |
|
|
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 15.09.2008, 20:39 Titel: |
|
|
Hi hamlet,
| hamlet hat Folgendes geschrieben: |
delikat erschien mir eine Verletzung der Invarianz gegenüber Spiegelungen, ich dachte dabei, ggf. falsch herum, an das Noether-Theorem. |
Invarianz gegenüber Spiegelung bedeutet lediglich, dass das Spiegelbild der obigen Skizze ebenfalls mögliche Lichtwege darstellt. Das ist hier der Fall.
Bei einer Glaslinse ist es ja ganz analog: Parallel einfallendes Licht wird zur optischen Achse hin abgelenkt. Auf einer Seite der Linse hat man eine ebene Welle auf der anderen eine Kugelwelle. Dennoch ist die Spiegelsymmetrie nicht verletzt, weil das Licht ebenso gut von der anderen Seite parallel einfallen könnte und dann eben im anderen Brennpunkt zusammenläuft.
Gravitationslinsen haben übrigens keinen Brennpunkt. Sie zeigen sehr starke Aberration. Das ist der Grund, weshalb eine exakt hinter der Gravitationslinse angeordnete Punktquelle als Ring erscheint und nicht auf einen Punkt abgebildet wird.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 15.09.2008, 21:32 Titel: |
|
|
Ich möchte nicht zu eilig antworten, aber zwei für heute letzte Nachträge:
| Zitat: | | Die Krümmung der im unendlichen parallelen Strahlen wird um so stärker, je näher sie dem Ereignishorizont sind. |
Wir haben es mit realen Horizonten zu tun, können daher von 'Oberflächen' sprechen: Die Krümmung der im unendlichen parallelen Strahlen wird um so stärker, je näher sie der Oberfläche eines Körpers sind (näher geht nicht).
Wo ist hier die räumliche Unterscheidung tangentialer/radialer Anteil der Bewegung zur Störungsqelle, im Moment der größten Wirkung - bezüglich der Abbildung, also der Auswirkung gegenüber einem Betrachter?
| Zitat: | | Bei einer Glaslinse ist es ja ganz analog: Parallel einfallendes Licht wird zur optischen Achse hin abgelenkt. Auf einer Seite der Linse hat man eine ebene Welle auf der anderen eine Kugelwelle. Dennoch ist die Spiegelsymmetrie nicht verletzt, weil das Licht ebenso gut von der anderen Seite parallel einfallen könnte und dann eben im anderen Brennpunkt zusammenläuft. |
Natürlich, die Spiegelsymmetrie ist nicht verletzt, weil das Funktional dasselbe ist. Die Abstände aber sind nicht symmetrisch. Ebensowenig z.B. Chiralität und abgebildete Wellenlänge.
Aber wie gesagt, ich muß darüber nachdenken, um mir ein Urteil zu erlauben.
gruß h |
|
| Nach oben |
|
|
Joachim
Anmeldedatum: 20.02.2006
Beiträge: 1714
|
| Verfasst am: 16.09.2008, 12:47 Titel: |
|
|
| hamlet hat Folgendes geschrieben: | Wenn man z.B. Herleitung und Illustration der rwth Aachen folgt, scheint es so zu sein, daß der Beobachter auf der Erde für das zu messende delta von 1.75'' eine ausgezeichnete Position einnimmt.
|
Das ist übrigens beim Regenbogen nicht anders. Auf der Skizze dieser Seite scheint es auch so, als nehme das Mädchen eine ausgezeichnete Position ein. Es sind halt nur die Strahlen eingezeichnet, die in die Augen des Mädchens treffen. Andere Beobachter sehen den Bogen allerdings im selben Winkel.
Gruß,
Joachim
_________________
Relativitaetsprinzip.Info
(Nicht mehr in diesem Forum aktiv) |
|
| Nach oben |
|
|
Aragorn
Anmeldedatum: 23.06.2006
Beiträge: 1120
|
| Verfasst am: 16.09.2008, 14:25 Titel: |
|
|
| hamlet hat Folgendes geschrieben: | 
Es taucht die Frage auf: Hat der Beobachter sie (die Sterne) denn nicht vorher unter dem blauen Öffnungswinkel gesehen? Ist nicht die relative Änderung ortsabhängig unterschiedlich? |
In deiner Skizze ist das so. In deiner Skizze sind die Sterne auch nur nen Sonnendurchmesser von der Sonne entfernt. Die tatsächlichen Proportionen sehen gänzlich anders aus. Wenn du die Verhältnisse passender zeichnen würdest, wären der blaue und rote Winkel identisch.
| hamlet hat Folgendes geschrieben: |
Da die Sonne selbst tangentiale Lichstrahlen (in Bezug der Verbindunglinie Sonne-Mond-Erde bei Sonnenfinsternis) emittiert, könne diese 'Eigentangenten' die Funktion Tangierender von anderen Sternen übernehmen. Nimmt man also an, die Sonne erscheine daher qua selbst um einen Winkel von 2*1.75'' vergrößert? |
Jein, allerdings vermutl. weniger als 2*1,75" weil die Strahlen von der Sonnenoberfläche kommen und ein kleinere Potentialdifferenz durchlaufen als Strahlen aus dem Unendlichen.
Gruß Helmut |
|
| Nach oben |
|
|
hamlet
Anmeldedatum: 26.01.2008
Beiträge: 19
|
| Verfasst am: 16.09.2008, 17:26 Titel: |
|
|
Hallo Joachim, hallo Helmut,
wenn ich Eure Aussagen vergleiche,
Helmut:
| Zitat: | | Die Quelle sollte so weit entfernt sein, dass bei ihr die von der Sonne ausgehende Gravitation nicht mehr messbar ist. |
| Zitat: | | Andere Beobachter sehen den Bogen allerdings im selben Winkel. |
Aragorn:
| Zitat: | | ...vermutl. weniger als 2*1,75" weil die Strahlen von der Sonnenoberfläche kommen und eine kleinere Potentialdifferenz durchlaufen als Strahlen aus dem Unendlichen. |
erkenne ich, daß ihr euch darin einig seid, daß die Position des Experimentators eine beliebige sein kann, er wird stets den gleichen Effekt messen.
Das heißt, daß auch bei der Finsternis einer sehr nahen Sonne (bei der meine Blickrichtung zum Sonnenrand über den Mondrand immer mehr tangential zur Oberfläche meines Planeten wird) ich die gleiche, weil lokal verursachte Abweichung messe. Einzige Voraussetzung ist die Tangente einer weit entfernten Quelle.
Wie sind aber die allgemeinen Relationen der lokalen Bedingungen?
Ich habe es so verstanden, daß die allgemeine Beschreibbarkeit, die faktische Invarianz eines zugrundeliegenden Phänomens idealerweise über einen geeigneten (richtigen) Tensor beschrieben wird, dieses elegante Werkzeug.
Je näher ich der Sonne komme, desto stärker stelle ich eine allgemeine Rot-Blau-Verschiebung fest, ich stelle also fest, daß meine Eigenzeit mit dem Abstand zur Sonne gegenüber "Außen" eine Veränderung erfährt. Eigenzeit ist vielleicht DAS elementare Prinzip von Relativität, und quasi trivial bedingt sie Lokalität. Ist sie hier oder überhaupt irgendwo in ihrer allgemeinen Bedeutung vernachlässigbar?
Nach einem Tensor, der zu dieser Frage eine schöne Zahl liefert, suche ich, und ich bin optimistisch, darin Energie, Winkel und Abstände zu finden, die es erlauben, eine beliebige gegebene Situation mathematisch korrekt zu beschreiben. Die Physik ist ja, zum Glück, sehr penibel.
grüße h
P.S.: Penibel. Hat eigentlich Goedel auch die erkenntnistheoretische Grundlage der Physik, sagen wir, zumindest erschüttert? Sollte man eigentlich erwarten. Davon habe ich noch nie gelesen. Ich denke, die Widerspruchsfreiheit eines kompletten mathematischen Hilbert-Weltbildes wird gerade so weit von 1 abweichen, wie es physikalische Unschärfe als Prinzip gibt. |
|
| Nach oben |
|
|
pauli
Anmeldedatum: 13.06.2007
Beiträge: 1551
|
| Verfasst am: 16.09.2008, 19:34 Titel: |
|
|
verstehe nur Bahnhof  |
|
| Nach oben |
|
|
|
|
Du kannst keine Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum nicht antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
|
|
FAQ
Suchen
Mitgliederliste
Benutzergruppen
Registrieren
Profil
Einloggen, um private Nachrichten zu lesen
Login
