Wolfgang Engelhardt und sein Unsinn mit dem Michelson-Interferometer

von Redaktion am 7. September 2014

Engelhardt-Unsinn, Folge 3: Als eingefleischter Einstein-Widerleger hat Dr. Engelhardt ein Problem mit dem Michelson-Morley Experiment, wie viele andere selbsternannte Widerleger auch. Widerspricht doch das Experiment der Hypothese eines absoluten Lichtäthers. Schon Prof. Thim hat versucht das Michelson-Morley Resultat mit nichtrelativistischer Physik zu beschreiben. Die Erklärung von Engelhardt weist noch haarsträubendere Fehler auf als jene von Prof. Thim.

Die Widerlegung von Engelhardt datiert vom Mai 2011. Offenbar war ihm dessen Absurdität bewusst, denn entgegen seiner sonstigen Gepflogenheit publizierte er diese nicht bei Arxiv.org sondern nur auf der kürzlich gehackten Webseite der NPA. RelativKritisch hat sich schon mehrfach mit Dr. Engelhardt beschäftigt und ihm nicht nur zwei Artikel gewidmet, sondern auch einen Gastbeitrag von ihm veröffentlicht. Alle drei Beiträge wurden kontrovers diskutiert. Dr. Engelhardt hat konsequent jede Kritik ignoriert und an allen seinen fehlerhaften Argumenten festgehalten. Dr. Engelhardt erweist sich damit als Prototyp des „Scientific cranks“. Egal, wie absurd und haarsträubend seine Fehler auch sein mögen, was er sagt, ist aus seiner eigenen Sicht immer richtig. Mit seiner Widerlegung des Michelson-Morley Ergebnisses wird jedoch offensichtlich, was kaum jemand noch in Zweifel gezogen hat. Dr. Engelhardt ist ein Crank wie er im Buche steht. Er ignoriert und verdreht Fakten ohne jede Rücksicht und wider besseren Wissens, mit dem einzigen Ziel, seine pseudowissenschaftliche Anti-Einstein-Propaganda voranzutreiben.

Abb. 1: Engelhardt, W., „Phase and Frequency Shift in a Michelson Interferometer,“ Natural Philosophy Alliance, 2011 (PDF-Dokument)

In der Zusammenfassung seiner Widerlegung schreibt Engelhardt (siehe Abb. 1, Übersetzung durch die Redaktion):

In dieser Arbeit wird gezeigt, dass eine klassische mechanische Trägertheorie – sei es für Licht oder sei es für Schall – tatsächlich das beobachtete Nullresultat vorhersagt. Michelson erwartete eine Verschiebung der Interferenzringe, wenn sein Interferometer im „Ätherwind“ gedreht wird. Eine solche Phasenänderung erfordert jedoch eine vorübergehende Frequenzänderung in einem der Arme des Interferometers. Da der „Ätherwind“ die Frequenz im Interferometer nicht ändert, kann sich auch keine Phasenverschiebung auftreten.

Engelhardts Behauptung, dass eine Phasenänderung eine vorübergehende Änderung der Länge der Interferometerarme erfordert, ist schlicht Unsinn. Das Michelson-Interferometer soll Lichtlaufzeitdifferenzen zwischen den beiden Armen des Interferometers messen, die durch den „Ätherwind“ verursacht werden – wenn es einen solchen gibt. Der „Ätherwind“ bestimmt die Lichtgeschwindigkeit in den Armen und damit die Laufzeit. Die Frequenz des Lichts bestimmt der Sender, also die Lichtquelle. Ganz allgemein sendet der Sender (angenommen bei x=0) ein Signal f(t), das sich ungedämpft in Richtung der x-Achse mit der Geschwindigkeit c ausbreitet (siehe Abb. 2).

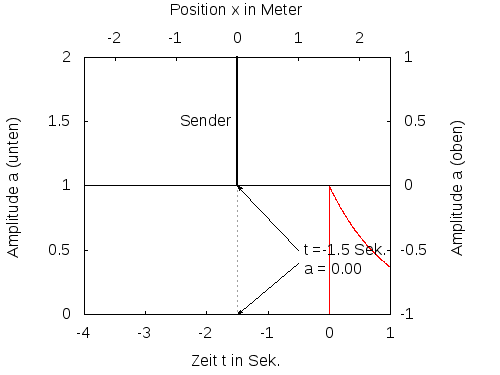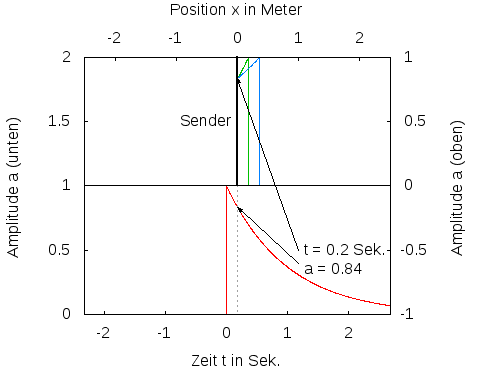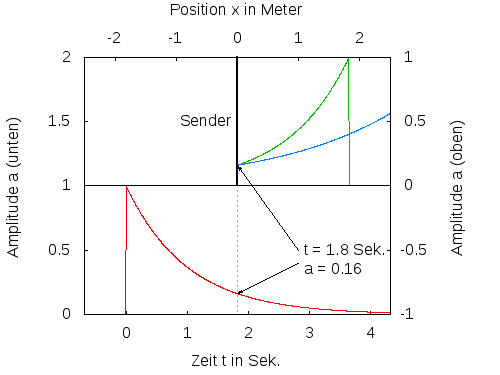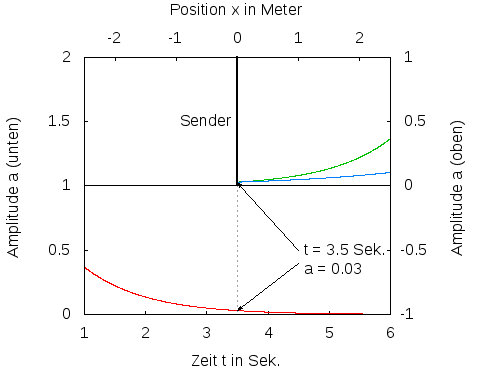
Abb. 2: Ein Sender sendet einen Impuls, der sich mit unterschiedlicher Geschwindigkeit ausbreitet. Die rote Kurve zeigt den zeitlichen Verlauf des gesendeten Signals. Die grüne und die blaue Kurve zeigen die sich in x-Richtung bewegenden Impulse. Der blaue Impuls bewegt sich doppelt so schnell wie der grüne.

An einer beliebigen Stelle x>0 kommt das Signal nach einer gewissen Laufzeit T(x) später an. Ein Empfänger detektiert dann eine Signal f(t-T(x)). Läuft das Signal auf dem Weg vom Sender zum Empfänger mit der konstanten Geschwindgkeit c, ergibt sich T(x)=x/c und damit f(t-x/c). Macht man zu einem bestimmten Zeitpunkt t eine Momentaufnahme des Signals, so erhält man z.B. für t=0 den örtlichen Verlauf des Signals mit f(-x/c). Das ist das gespiegelte und mit 1/c skalierte gesendete Signal, je nach Zeitpunkt mehr oder weniger weit nach rechts verschoben. Je grösser die Geschwindigkeit c ist, um so mehr wird das Signal gedehnt und um so früher kommt es bei Empfänger an (siehe Abb. 2). Die Funktion

$\displaystyle \tilde{f}(t,x)=f(t-\frac{x}{c})$

(1)

ist übrigens eine allgemeine Lösung der homogenen Wellengleichung

$\displaystyle \frac{\partial^2 \tilde{f}}{\partial x^2}-\frac{1}{c^2}\,\frac{\partial^2 \tilde{f}}{\partial t^2}=0,$

(2)

wie man durch Nachrechnen prüfen kann.

Für das Michelson-Interferometer wurde nun monochromatisches Licht, also eine harmonische Schwingung, als Signal verwendet mit dem auch Dr. Engelhardt seine Rechnung durchgeführt hat:

$\displaystyle f(t)=-A\sin(\omega t)=A\sin(-\omega t).$

(3)

Beim Empfänger an der Stelle x>0 erhalt man damit

$\displaystyle f(t-\frac{x}{c})=-A\sin(\omega(t-\frac{x}{c}))=A\sin(-\omega(t-\frac{x}{c}))$

(4)

und weiter

$\displaystyle A\sin(-\omega(t-\frac{x}{c}))=A\sin(\frac{\omega}{c}x-\omega t)=A\sin(kx-\omega t)$

(5)

Wobei

$\displaystyle k=\frac{\omega}{c}=\frac{2\pi}{\lambda}$

(6)

der Wellenvektor ist. $\lambda=2\pi c/\omega$ ist die Wellenlänge, die bei vom Sender vorgegebener Kreisfrequenz $\omega$ von der Geschwindigkeit $c$ abhängt. Je grösser $c$ ist, um so grösser ist die Wellenlänge $\lambda$ (siehe Abb. 3).

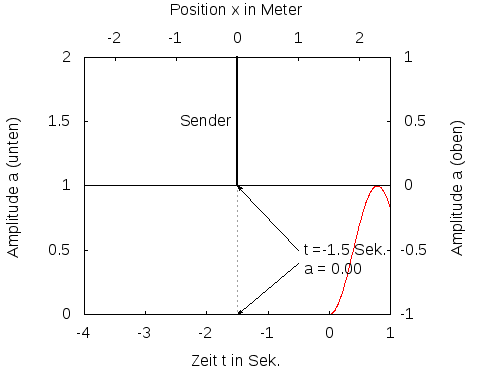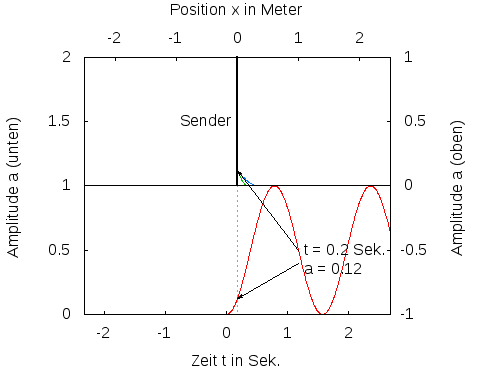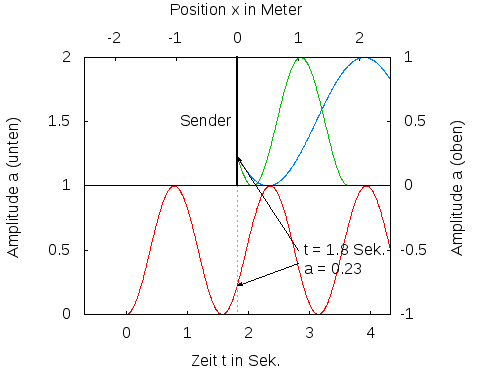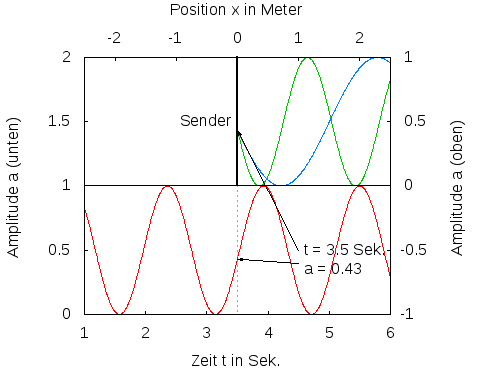
Der Sender sendet ein Sinussignal mit der Frequenz ω (rote Kurve), das sich mit unterschiedlicher Geschwindigkeit ausbreitet (grüne und blaue Kurve). Das blaue Signal läuft doppelt so schnell wie das rote Signal und hat daher die doppelte Wellenlänge.

Abb. 3: Der Sender sendet ein Sinussignal mit der Frequenz ω (rote Kurve), das sich mit unterschiedlicher Geschwindigkeit ausbreitet (grüne und blaue Kurve). Das blaue Signal läuft doppelt so schnell wie das rote Signal und hat daher die doppelte Wellenlänge.

Die Phasenverschiebung zwischen gesendetem und empfangenem Signal in einem Interferometerarm mit der Länge L erhält man mit dem mittleren Term in Gl. (4) zu

$\displaystyle -A\sin(\omega(t-\frac{2L}{c_i}))=-A\sin(\omega t - \varphi_i),$

(7)

$\displaystyle \varphi_i=2L\frac{\omega}{c_i}=4\pi L\frac{1}{\lambda_i},$

(8)

wobei $c_i$ die mittlere Geschwindigkeit im jeweiligen Arm des Interferometers ist. Zwischen den beiden Signalen mit den Geschwindigkeiten $c_1$ und $c_2$ ergibt sich dann eine Phasendifferenz von

$\displaystyle \Delta\varphi=\varphi_1-\varphi_2=2L\omega(\frac{1}{c_1}-\frac{1}{c_2})=4\pi L(\frac{1}{\lambda_1}-\frac{1}{\lambda_2}).$

(9)

Wird das Interferometer um 90° gedreht, wird $\Delta\varphi$ zu $-\Delta\varphi$ und die gesamte Phasenverschiebung für die Interferenzringe ergibt sich zu $\Delta\phi=2\Delta\varphi$ .

Dr. Engelhardt behauptet nun, dass $\Delta\phi=0$ sein muss, da $\lambda$ von der Signalgeschwindigkeit unabhängig sei ( $\lambda_1=\lambda_2=\lambda$ ) und führt dazu in seiner Widerlegung einen geradezu aberwitzigen „Beweis“ an (siehe Abb. 4).

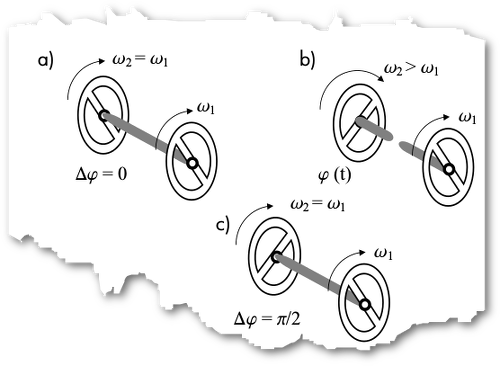
Unbrauchbares Räderbeispiel von Engelhardt auf Seite 4 in „Phase and Frequency Shift in a Michelson Interferometer,“ Natural Philosophy Alliance, 2011

Abb. 4: Unbrauchbares Räderbeispiel von Engelhardt auf Seite 4 in „Phase and Frequency Shift in a Michelson Interferometer,“ Natural Philosophy Alliance, 2011 (siehe Abb. 1)

Er vergleicht dazu den Sachverhalt im Interferometer mit den beiden Rädern auf einer Achse. Doch die Räder auf der Achse haben eine fixe „Wellenlänge“, nämlich ihren Umfang. Der ändert sich naturgemäss nicht, wenn das Auto schneller oder langsamer fährt. Deshalb müssen sich die Räder schneller drehen (eine höhere Frequenz haben), wenn das Auto schneller fährt. Beim Interferometer hängt die Wellenlänge jedoch sehr wohl von der Signalgeschwindigkeit ab (siehe Gl. (8)). Engelhardts „Beweis“ ist völlig unbrauchbar und seine Widerlegung löst sich in Luft auf.

Damit zeigt Dr. Engelhardt einmal mehr, dass ihm für seine Crackpot-Physik kein Unsinn zu absurd ist. Mit Wissenschaft haben seine Pamphlete nichts zu. Was Dr. Engelhardt bewegt, diesen Nonsens zu veröffentliche, obwohl er es als promovierter Physiker besser wissen muss, bleibt jedem selbst überlassen zu beurteilen.

Diskutiere mit anderen Benutzern über Wolfgang Engelhardt und seinen Unsinn über das Michelson-Interferometer im Forum Alpha Centrauri

RelativKritisch E-Edition

Als ePub herunterladen 4611

Die Artikel von RelativKritisch gibt es auch als E-Book im ePub-Format zum kostenlosen Download!

Ähnliche Beiträge

Kategorien: Aussenseiter

Permalink Trackback

Vorheriger Beitrag

Nächster Beitrag

2.631 Kommentare | Kommentar schreiben

#2601 | Martin Raible | 5. Mai 2018, 02:20

Redaktion schrieb am 4. März 2018, 20:41:

Martin Raible,

Wolfgang Engelhardt versucht gerade bei Markus Pössel Ihre Diskussionsbeiträge zur Berechnung des Merkur-Perihels zu diskreditieren.

Beste Grüsse
RelativKritisch Redaktion

Danke für diesen Hinweis. Ich war nach einem Umzug im Januar fast vier Monate lang ohne Internet und habe deswegen erst vor drei Tagen reagiert.

Diesen Kommentar: Zitieren
#2602 | Dr. Wolfgang Engelhardt | 26. Mai 2018, 18:58

Martin Raible schrieb am 5. Mai 2018, 02:20:

Redaktion schrieb am 4. März 2018, 20:41:

Martin Raible,

Wolfgang Engelhardt versucht gerade bei Markus Pössel Ihre Diskussionsbeiträge zur Berechnung des Merkur-Perihels zu diskreditieren.

Beste Grüsse
RelativKritisch Redaktion

Danke für diesen Hinweis. Ich war nach einem Umzug im Januar fast vier Monate lang ohne Internet und habe deswegen erst vor drei Tagen reagiert.

Ich habe bei Scilog Raible’s Rechnungen bestätigt, nicht „diskreditiert“. Allerdings sperrt mich dort Pössel. Hier meine Antworten auf diverse Beiträge von Raible:

@Raible (21.Mai, 3h22)
Nun finden Sie also, dass Einsteins (11 E) exakt aus der Schwarzschild-Metrik folgt und B die Bedeutung von (10 E) hat. Beides hat Poessel energisch bestritten. Weil er keine Argumente hatte, musste er mich in seiner Hilflosigkeit sperren.

Haben Sie eine Erklärung, warum Gerber Einsteins (14 E) vorausahnen konnte, obwohl Gerber die falschen Voraussetzungen hatte und sich dazu noch verrechnete?

@Raible (21. Mai, 22h18)
Nun verwenden Sie also auch Schwarzschilds (15) mit h=1, wie es aus (14) auch folgt und Chrys nicht mehr bestreitet. Dann folgt aus Vergleich von Schwarzschilds (18) mit Einsteins (11) A=0 <<<1.

Warum machen Sie es sich so schwer, aus der Lehrbuchgleichung (2) in meinem Papier über (6) Einsteins (11 E) zu erhalten. Allerdings müssen Sie noch eine physikalische Begründung finden, warum Sie C^2=1+2 A setzen sollen und nicht C^2=1 wie es bei Schwarzschild folgt, weil A=0 gilt.

Diesen Kommentar: Zitieren
#2603 | Noblinsiki | 4. Juni 2018, 18:45

Hallo und guten Tag!
Ich muss das mal hier einfügen: http://www.pro-physik.de/details/news/11063484/Positiver_Null-Test.html

Versteht das hier jemand? Ist das nicht das Gegenteil von dem, was hier lang und breit diskutiert wurde?

Diesen Kommentar: Zitieren
#2604 | Noblinski | 5. Juni 2018, 09:52

Ich habe tatsächlich meinen berühmten Namen oben falsch geschrieben. Wenn das nicht das Symptom einer heimtückischen Krankheit ist. Wahrscheinlich liegt es an meinem „Mausarm“, denn ich muss vorwiegend mit der linken Hand, und die ist noch ungeschickter als meine rechte…

Ich hätte auch nicht „einfügen müssen“ – ich wollte. Denn offenbar hat der Mond, der bekanntermaßen nicht stille am Himmel steht, keinen Einfluss auf ein Dutzend zwanglos auf der Erdoberfläche verteilte Atomuhren. Während er gleichzeitig die Massen der Ozeane locker zweimal am Tag 4-6m in die Höhe treiben kann. Also momentan gehe ich noch davon aus, dass ich da etwas nicht verstanden habe. Hallo Prof. Einstein (selig)! Man kann also kreisende Uhren höchster Genauigkeit problemlos dauerhaft synchronisieren. Sakrament!!

Diesen Kommentar: Zitieren
#2605 | Noblinski | 27. Juni 2018, 08:15

Falls die Redaktion von Relativ Kritisch inzwischen verstorben ist, wäre es doch Zeit nun für einen Nachruf.

Diesen Kommentar: Zitieren
#2606 | Redaktion | 5. Juli 2018, 23:12

Noblinski,

Sie sind besser beraten, sich um Ihre eigene Gesundheit zu sorgen.

Beste Grüsse
RelativKritisch Redaktion

Diesen Kommentar: Zitieren
#2607 | Noblinski | 6. Juli 2018, 01:04

Das tue ich. Es ist schön, zu lesen, dass Sie wohlauf sind. Ich hatte schon Bedenken, dieses Forum würde von vagabundieren Einfalltspinseln übernommen.
Beste Grüße!

Diesen Kommentar: Zitieren
#2608 | Noblinski | 6. Juli 2018, 01:06

Das tue ich. Es ist schön, zu lesen, dass Sie wohlauf sind. Ich hatte schon Bedenken, dieses Forum würde von vagabundierenden Einfalltspinseln übernommen.
Beste Grüße!

Diesen Kommentar: Zitieren
#2609 | Noblinski | 6. Juli 2018, 08:08

Einfalt schreibt man genau wie Dreifältigkeit mit nur einem l. Zwiefältigkeit gibt es nicht, bloß Bifurkation. Liebe Redaktion, ich muss mich für meine Penetranz hier entschuldigen. Aber schauen Sie in Ihren eigenen Leitfaden, da steht, dass ich hier mit meiner Einstein- Skepsis genau richtig bin. Warum hat sich das hoch geachtete Genie in über 50 Jahren nie dazu geäußert, weshalb es nach den elementarsten Gesetzen der Logik so aussieht, als würden die beiden Uhren gleich schnell gehen? Warum die auf den ersten Blick absurde Vorstellung, aus der Verzögerung eines Lichtstrahls bei einer Messung auf die reale Verzerrung von Raum und Zeit zu schließen? Ich glaube nicht, dass Einstein das übersehen hat. Er muss vielmehr gute Gründe gehabt haben, das zu verschweigen. Vielleicht politische?

Diesen Kommentar: Zitieren
#2610 | Noblinski | 1. Oktober 2018, 11:43

Meine Fassung des Ergebnisses des Michelson-Morley-Experiments: Bei Durchgang durch halbdurchlässige und der Reflexion an idealen Spiegeln (aber auch durch Linsen) verändert sich die Frequenz des verwendeten Lichtes in Abhängigkeit der Bewegung dieser optischen Bauteile. Bewegt sich ein Spiegel auf die Quelle des Lichtes zu, verkürzt sich die Frequenz um einen Betrag, der von der Geschwindigkeit und dem Sinus des Einstrahlwinkels zur Bewegungsrichtung abhängt. Im Falle der 90°-Spiegelanordnung beim besagten Experiment ist die Summe beider Sinusse immer gleich 1. Das Experiment kann sich also im Raum drehen, wie man will, die Effekte der Veränderungen im geteilten Strahl überlagern sich in jedem Falle auf dasselbe Ergebnis. Wie man ja auch beobachtet. Das ist ja wahrsscheinlich auch der tiefere Grund, warum man in den heutigen großen Gravitationswellendetektoren andere Wege gegangen ist. Voila!

Diesen Kommentar: Zitieren
#2611 | Noblinski | 1. Oktober 2018, 14:08

Nachtrag: Es verkürzt sich natürlich die Wellenlänge, die Frequenz muss sich also erhöhen. Auf dem Rückweg durch den Strahteiler umgekehrt. Dessen anfänglicher Einfluss hebt sich also bis auf einen kleinen Rest auf.
Beste Grüße!

Diesen Kommentar: Zitieren
#2612 | Redaktion | 1. Oktober 2018, 14:53

Noblinski schrieb am 1. Oktober 2018, 11:43:

Meine Fassung des Ergebnisses des Michelson-Morley-Experiments: Bei Durchgang durch halbdurchlässige und der Reflexion an idealen Spiegeln (aber auch durch Linsen) verändert sich die Frequenz des verwendeten Lichtes in Abhängigkeit der Bewegung dieser optischen Bauteile. Bewegt sich ein Spiegel auf die Quelle des Lichtes zu, erhöht sich die Frequenz um einen Betrag, der von der Geschwindigkeit und dem Sinus des Einstrahlwinkels zur Bewegungsrichtung abhängt. …

Beim Michelson-Morley-Experiment bewegen sich Quelle, Strahlteiler, Spiegel und Detektor zueinander aber nicht. Sie sind relativ zueinander in Ruhe.

Diesen Kommentar: Zitieren
#2613 | Noblinski | 1. Oktober 2018, 17:29

Redaktion schrieb am 1. Oktober 2018, 14:53:

Beim Michelson-Morley-Experiment bewegen sich Quelle, Strahlteiler, Spiegel und Detektor zueinander aber nicht. Sie sind relativ zueinander in Ruhe.

Ja, klar. Aber auf den Ursprungsort des Lichtes im Vakuum bezogen bewegen sie sich doch. Der Ort auf der Erdbahn, wo das betrachtete Photon innerhalb einer (oder zwei) Pikosekunden vom angeregten Elektron ins Vakuum springt.

Diesen Kommentar: Zitieren
#2614 | Noblinski | 2. Oktober 2018, 08:57

Ich nehme jetzt mal Ihren Einwand vorweg, ich hätte noch gar nicht verstanden, dass es bei Michelson-Morley um die Laufzeiten geht und nicht um Frequenzen. Davon hatte ich abstrahiert, ohne es zu erwähnen, Entschuldigung! Es geht ja um den Beweis der Isotropie der Lichtgeschwindigkeit. Und da ist es so, dass sich nicht etwa die Lichtstrahlen bzw. Teilstrahlen in der Apparatur bewegen, sondern sie bewegen sich im Vakuum, und die Apparatur wird quasi mit nicht genau bekannter Geschwindigkeit und Richtung darüber hinweg gezogen. Für die Verzögerung des Lichts zwischen beiden Wegen gilt genau dasselbe: Sie hängt ab von den Sinussen der Winkel zwischen Licht und Bewegungsrichtung, und die addieren sich bei um 90° versetzten Kanälen immer zu 1. Alle dadurch erzeugten Interferenzbilder sind gleich, weshalb die Versuchsanordnung nicht geeignet ist, eine eventuelle Anisotropie von Licht nachzuweisen.
–
Weiterhin hatten wir hier schon mal in der Rede über das Sagnac-Interferometer den sachkundigen Einwand von Philip, dass sich überlagerte phasenverschobene Teilstrahlen, was die longitudinale Komponente angeht, nicht von einer Welle unterscheiden, die in der selben Form als Einzelwelle erzeugt wurde. Daraus folgt, dass es eben nicht die Aspekte der longitudinalen Phasenverschiebung sind, die letztlich das beobachtete Interferenzbild erzeugen. (Auch nicht, wenn man damit sehr präzise Längenmessungen machen kann.) Sondern es sind die sonstigen im Raum verteilten Unterschiede zwischen beiden Stahlen, die in den Unterschieden ihrer Geschichte liegen, wie etwa die geringfügig verschobene Frequenz.

Diesen Kommentar: Zitieren
#2615 | Martin Raible | 23. Oktober 2018, 23:41

Ich habe einen Artikel mit dem Titel „Energy constants in Einstein’s explanation of the perihelion motion of Mercury“ hier hinterlegt. Darin erkläre ich, warum A_E=A sein kann. Ich erkläre auch, warum A_E=A/(1-2A) sein kann, schreibe aber, dass man diese Relation nicht beweisen kann, da man nicht lambda_2=0 beweisen kann. Ich komme zu diesen Ergebnissen, indem ich die DGL für u² durch sukzessive Approximationen löse. Die n-te Approximation von u² enthält alle Terme erster bis n-ter Ordnung in A, alpha/r und B²/r².

@Chrys:
Sie haben am 1. Juni 2018, 16:31 Uhr und am 7. Juni 2018, 14:30 Uhr zu beweisen versucht, dass A_E=A/(1-2A) ist. Beide Male haben Sie die Gleichung u²-alpha/r=2A+O(alpha/r) verwendet, wobei O(alpha/r) wohl für Terme stehen soll, die den Faktor alpha/r enthalten. Zwischendurch habe ich am 2. Juni 2018, 00:55 Uhr aufgeschrieben, dass ich mit dieser Gleichung nicht einverstanden bin.

Ich bin also mit der Gleichung u²-alpha/r=2A+O(alpha/r) nicht einverstanden. Sie bedeutet, wenn Sie mit meinem oben verlinkten Artikel vergleichen, dass in der n-ten Approximation von u² die Koeffizienten lambda_2, lambda_3, …, lambda_n alle gleich null sein müssen. Und dafür gibt es keinen Grund.

Diesen Kommentar: Zitieren
#2616 | Martin Raible | 31. Oktober 2018, 02:57

In dem im vorhergehenden Beitrag von mir verlinkten Artikel wird also die Gleichung $\frac{dx_i}{ds}\left(\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}\right)=0$ gelöst, wobei i die Werte 1,2,3 durchläuft, $\mu$ und $\nu$ dagegen die Werte 0,1,2,3 durchlaufen. Da stellt sich die Frage, ob aus der Gleichung $\frac{d^2x_\tau}{ds^2}+\Gamma^\tau_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ mit $\tau=0,1,2,3$ weitere Informationen folgen, die die Wahl der Koeffizienten $\lambda_n$ mit $n=2,3,4,\ldots$ in jenem Artikel weiter einschränken. Ich werde im Folgenden zeigen, dass es nicht so ist.

1) Zunächst betrachte ich den Fall einer nicht kreisförmigen Planetenbahn: Da $r^2\frac{d\phi}{ds}H=B$ konstant ist, sind auch die Größen $\left(x_i\frac{dx_j}{ds}-x_j\frac{dx_i}{ds}\right)H$ mit $i,j\in\{1,2,3\}$ konstant. Daraus folgt durch Ableitung nach s: $x_i\left(\frac{d^2x_j}{ds^2}+\Gamma^j_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}\right)-x_j\left(\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}\right)=0$ für alle $i,j\in\{1,2,3\}$ . Und daraus folgt $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=Kx_i$ für alle $i\in\{1,2,3\}$ . Aus $\frac{dx_i}{ds}\left(\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}\right)=0$ folgt daher $Kx_i\frac{dx_i}{ds}=0$ . Ist $r\frac{dr}{ds}=x_i\frac{dx_i}{ds}\neq 0$ , so ist daher $K=0$ , so dass wir $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ für alle $i\in\{1,2,3\}$ haben. Die Gleichung $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ für alle $i\in\{1,2,3\}$ gilt also in jedem Bahnabschnitt zwischen einem Perihel und einem Aphel. Aus dem 1. Mittelwertsatz der Differentialrechnung und der Stetigkeit von $\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}$ als Funktionen von s folgt dann, dass $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ auch an einem Perihel oder Aphel und daher auf der gesamten Bahn für alle $i\in\{1,2,3\}$ gilt.

2) Nun betrachte ich den Fall einer kreisförmigen Planetenbahn: Eine solche kreisförmige Bahn wird von einer Lösung der Gleichung (4.14) des oben von mir verlinkten Artikels vorhergesagt, wenn $\left(\frac{dr}{ds}\right)^2=u^2-\frac{B^2}{r^2H^2}$ als Funktion von r ein lokales Maximum hat, bei dem $\left(\frac{dr}{ds}\right)^2=0$ gilt. Aus der Maximumseigenschaft folgt $\frac{du^2}{dr}-\frac{2B^2H'}{r^2H^3}\frac{\alpha}{r^2}+\frac{2B^2}{r^3H^2}=0$ bei jenem r. Aus Gleichung (4.8) des oben von mir verlinkten Artikels folgt nach Multiplikation mit $2\frac{ds}{dr}$ eine Gleichung, die von einer Lösung der Gleichung (4.14) erfüllt wird und im Falle $\frac{dr}{ds}=0$ die Form annimmt: $\frac{du^2}{dr}-\frac{F'}{G+H}\frac{\alpha}{r^2}\left(\frac{dt}{ds}\right)^2+\frac{2G}{G+H}\frac{u^2}{r}+\frac{H'}{G+H}\frac{\alpha}{r^2}u^2-\frac{2H'}{H}\frac{\alpha}{r^2}u^2=0$ . Gleichsetzen beider Ausdrücke für $\frac{du^2}{dr}$ und Ausnutzen der Beziehung $u^2=\frac{B^2}{r^2H^2}$ ergibt: $\frac{u^2}{r}=-\frac{1}{2}\frac{F'}{G+H}\frac{\alpha}{r^2}\left(\frac{dt}{ds}\right)^2+\frac{G}{G+H}\frac{u^2}{r}+\frac{1}{2}\frac{H'}{G+H}\frac{\alpha}{r^2}u^2$ . Für eine gleichförmige Kreisbewegung gilt nun: $\frac{d^2x_i}{ds^2}=-\frac{u^2}{r}\frac{x_i}{r}$ für alle $i\in\{1,2,3\}$ . Daraus folgt daher: $\frac{d^2x_i}{ds^2}=\frac{1}{2}\frac{F'}{G+H}\frac{x_i}{r}\frac{\alpha}{r^2}\left(\frac{dt}{ds}\right)^2-\frac{G}{G+H}\frac{x_i}{r}\frac{u^2}{r}-\frac{1}{2}\frac{H'}{G+H}\frac{x_i}{r}\frac{\alpha}{r^2}u^2$ . Und daraus folgt mit Gleichung (4.4) des oben von mir verlinkten Artikels, dass $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ für alle $i\in\{1,2,3\}$ gilt.

Somit erfüllen die Lösungen von Gl. (4.14) die Gleichung $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ für alle $i\in\{1,2,3\}$ . Jetzt bestimmen wir aus $u^2$ mit Hilfe von Gl. (4.11) die Größe $\left(\frac{dt}{ds}\right)^2$ . Dann ist Gl. (4.10) erfüllt. Es gilt also $g_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=const=1-2A$ . Daraus folgt durch Ableitung nach s: $g_{\mu\nu}\frac{dx_\mu}{ds}\left(\frac{d^2x_\nu}{ds^2}+\Gamma^\nu_{\sigma\tau}\frac{dx_\sigma}{ds}\frac{dx_\tau}{ds}\right)=0$ . Und da wir schon wissen, dass $\frac{d^2x_i}{ds^2}+\Gamma^i_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ für alle $i\in\{1,2,3\}$ ist, folgt $\frac{d^2t}{ds^2}+\Gamma^0_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ . Aus der Gleichung $\frac{d^2x_\tau}{ds^2}+\Gamma^\tau_{\mu\nu}\frac{dx_\mu}{ds}\frac{dx_\nu}{ds}=0$ mit $\tau=0,1,2,3$ folgen daher keine weiteren Informationen, die die Wahl der $\lambda_n$ mit $n=2,3,4,\ldots$ in dem oben verlinkten Artikel einschränken.

Diesen Kommentar: Zitieren
#2617 | Martin Raible | 9. Dezember 2018, 23:39

Martin Raible schrieb am 18. Januar 2017, 18:00:

Leider muss an dieser Stelle aber gesagt werden, dass Einsteins Gl. (7bE) tatsächlich falsch ist. Gl. (7bE) ist falsch, weil Gl. (9E) falsch ist. Bei der Herleitung von Gl. (9E) hat Einstein eine eine Zeile weiter oben stehende Differentialgleichung integriert und dabei der Integrationskonstanten einen falschen und willkürlichen Wert zugewiesen.

Ich muss mich hier korrigieren: Die Zeitvariable s in Einsteins Gleichung (7) ist nicht die Eigenzeit, sondern die Eigenzeit multipliziert mit einem frei wählbaren konstanten Faktor, der allerdings nicht null sein darf. Deshalb ist die Integrationskonstante bei der Integration der DGL, die oberhalb von Einsteins Gl. (9) steht, frei wählbar. Einsteins Gl. (9) und damit auch Einsteins Gl. (7b) sind daher korrekt.

Ich muss deswegen nicht Dr. Engelhardts Aufforderung folgen, einen Artikel mit meiner „Korrektur“ zu Einsteins Perihel-Paper zu veröffentlichen.

Diesen Kommentar: Zitieren
#2618 | Noblinski | 11. April 2019, 14:22

Die Fotografie des Schwarzen Loches im 1,3mm Mikrowellenbereich war möglich „nachdem alle beteiligten Teleskope auf 1 Nanosekunde genau synchronisiert wurden“ (Quelle DPG).

Diesen Kommentar: Zitieren
#2619 | Martin Raible | 27. September 2019, 03:47

Martin Raible schrieb am 23. Oktober 2018, 23:41:

Ich habe einen Artikel mit dem Titel „Energy constants in Einstein’s explanation of the perihelion motion of Mercury“ hier hinterlegt. Darin erkläre ich, warum A_E=A sein kann. Ich erkläre auch, warum A_E=A/(1-2A) sein kann, schreibe aber, dass man diese Relation nicht beweisen kann, da man nicht lambda_2=0 beweisen kann. Ich komme zu diesen Ergebnissen, indem ich die DGL für u² durch sukzessive Approximationen löse. Die n-te Approximation von u² enthält alle Terme erster bis n-ter Ordnung in A, alpha/r und B²/r².

Ich habe einen einfacheren Lösungsweg gefunden. Aus Gl. (4.1) meines Artikels und der Geodätengleichung folgt, dass $\frac{dt}{ds}F=C$ eine Konstante ist. Es ist also $\frac{dt}{ds}=C/F$ . Setzt man das in Gl. (4.11) meines Artikels ein und löst nach $u^2$ auf, so erhält man
$u^2=\frac{C^2-F}{F(G+H)}+\frac{2A}{G+H}+\frac{G}{(G+H)H^2}\frac{B^2}{r^2}$ . Dies ist die exakte Lösung von Gl. (4.14) meines Artikels, der DGL für $u^2$ . Aus Gl. (4.7) und (4.2) meines Artikels erhält man $F(\alpha/r)=1-\alpha/r+\mathcal{O}((\alpha/r)^3)$ . Setzt man außerdem $C^2=1+\lambda_2A^2+\lambda_3A^3+\lambda_4A^4+\ldots$ und die Gl. (4.2) meines Artikels ein, so erhält man bis auf Terme dritter und höherer Ordnung in $A$ , $\alpha/r$ und $B^2/r^2$ : $u^2=\left(\frac{\alpha}{r}+\lambda_2A^2\right)+\left(2A-2A\frac{\alpha}{r}\right)+\frac{\alpha}{r}\frac{B^2}{r^2}$ . 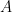Und das ist die Gl. (4.18) meines Artikels, die zweite Approximation von $u^2$ .

Diesen Kommentar: Zitieren
#2620 | Herr Senf | 27. September 2019, 10:08

Der link auf mega.nz geht, kommt aber drin nicht an’s Ziel.

Diesen Kommentar: Zitieren
#2621 | Martin Raible | 27. September 2019, 23:36

Herr Senf schrieb am 27. September 2019, 10:08:

Der link auf mega.nz geht, kommt aber drin nicht an’s Ziel.

Auf meinem Computer klappt’s. Aber vielleicht ja dies ans Ziel:
https://www.dropbox.com/sh/aomd2e6rq5yqrat/AAALkIXHm14g47dvUPgRFCtSa?dl=0

Diesen Kommentar: Zitieren
#2622 | galileo2609 | 28. September 2019, 21:00

Vielen Dank Martin Raible!

Grüsse galileo2609

Diesen Kommentar: Zitieren
#2623 | Martin Raible | 28. September 2019, 22:52

<a href="http://www.relativ-kritisch.net/blog/kritiker/wolfgang-engelhardt-unsinn-michelson-interferometer/comment-page-53#comment-33217" title="galileo2609 schrieb am 28. September 2019, 21:00″>galileo2609 schrieb am 28. September 2019, 21:00:

Vielen Dank Martin Raible!

Grüsse galileo2609

Ich wollte noch einmal sagen, worum es geht: In Einsteins Artikel über die Perihelbewegung des Merkur gibt es zwei Gleichungen, die die Konstante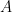 $A$ enthalten, nämlich Gl. (8) und die Gleichung, die unter der Gl. (7c) steht. Ich untersuche, ob es überhaupt richtig war, in beide Gleichungen die gleiche Konstante zu schreiben. Deshalb setze ich in die zweite Gleichung statt 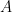$A$ erstmal eine Konstante $A_E$ ein. 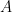Ich kann dann aber zeigen, dass $A_E$ und $A$ gleich sein können. Einstein hatte Recht, in beide Gleichungen die gleiche Konstante zu schreiben.

Ich habe das deswegen getan, weil auf dem Blog von Markus Pössel jemand behauptet hatte, er könne die Beziehung $A_E=\frac{A}{1-2A}$ beweisen.

Diesen Kommentar: Zitieren
#2624 | galileo2609 | 29. September 2019, 13:48

Hast du vor, Chrys deinen Lösungsweg auf Pössels LaTex-Spielwiese zur Verfügung zu stellen?

Grüsse galileo2609

Diesen Kommentar: Zitieren
#2625 | Martin Raible | 29. September 2019, 23:39

<a href="http://www.relativ-kritisch.net/blog/kritiker/wolfgang-engelhardt-unsinn-michelson-interferometer/comment-page-53#comment-33219" title="galileo2609 schrieb am 29. September 2019, 13:48″>galileo2609 schrieb am 29. September 2019, 13:48:

Hast du vor, Chrys deinen Lösungsweg auf Pössels LaTex-Spielwiese zur Verfügung zu stellen?

Grüsse galileo2609

Nein, diese vielen Gleichungen auf Pössels LaTex-Spielwiese einzugeben, ist mir zu mühsam.

Markus Pössel hatte mir im November 2018 gestattet, Chrys auf seinem Blog zu informieren, dass ich ihm auf RelativKritisch geantwortet habe, inklusive einem Link zu einem Artikel, den ich ins Internet gestellt habe.

Diesen Kommentar: Zitieren
#2626 | ralfkannenberg | 30. September 2019, 13:34

Martin Raible schrieb am 28. September 2019, 22:52:

Ich untersuche, ob es überhaupt richtig war, in beide Gleichungen die gleiche Konstante zu schreiben. Deshalb setze ich in die zweite Gleichung statt $A$ erstmal eine Konstante $A_E$ ein. Ich kann dann aber zeigen, dass $A_E$ und $A$ gleich sein können. Einstein hatte Recht, in beide Gleichungen die gleiche Konstante zu schreiben.

Hallo Martin,

diese Schlussfolgerung verstehe ich nicht: können sie gleich sein oder müssen Sie gleich sein ? Meines Erachtens folgt Dein 2.Satz aus dem ersten nur im 2.Fall.

Freundliche Grüsse, Ralf

Diesen Kommentar: Zitieren
#2627 | Martin Raible | 30. September 2019, 17:33

Hallo Ralf,

sie können gleich sein ( $A_E=A$ ), sie müssen es aber nicht. Auch die Gleichung $A_E=\frac{A}{1-2A}$ ist eine Möglichkeit. Diese Konstanten treten nämlich in zwei Approximationen (der ersten und der zweiten) und nicht in exakten Lösungen auf.

Ich hätte den 2. Satz anders formulieren müssen: Einstein beging keinen Fehler, in beide Gleichungen die gleiche Konstante zu schreiben.

Freundliche Grüsse, Martin

Diesen Kommentar: Zitieren
#2628 | ralfkannenberg | 30. September 2019, 23:41

Hallo Martin,

danke schön für Deine Klarstellungen.

Freundliche Grüsse, Ralf

Diesen Kommentar: Zitieren
#2629 | Martin Raible | 27. Dezember 2021, 04:12

Martin Raible schrieb am 19. April 2017, 09:15:

Dr. Wolfgang Engelhardt schrieb am 18. April 2017, 22:48:

Martin Raible schrieb am 18. April 2017, 02:20:

Da in $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ das alte $u^2$ und das alte B stehen, während in $u^2=2A+\alpha x+\alpha B^2x^3$ das neue $u^2$ und das neue B stehen, braucht $u^2=2A+\alpha x+\alpha B^2x^3$ die Gleichung $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ nicht zu lösen.

Es genügt mir völlig, Ihnen hier zu widersprechen.

Man kann aber diese Gleichung $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ lösen und findet nichts was dieser Gleichung $u^2=2 A +\alpha x+3 \alpha B^2x^3$ ähnelt. Einstein sagt noch nicht einmal, wie er die Bedeutung von B ändern will. Auf dieser Basis ist es unmöglich, irgendwelche belastbaren Schlüsse zu ziehen. Es ist also höchste Zeit, dass Sie Einstein’s Ungenauigkeiten bereinigen.

Mit Befriedigung stelle ich fest, dass Sie diese Gleichung $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ offenbar für richtig halten. Die Lösung überlasse ich Ihnen. Sie wird einen prominenten Platz in Ihrer Einstein-Apologie finden. So lange Sie aber diese Lösung gar nicht angeben, kann ich auch nicht nach Rechenfehlern suchen.

Ich habe $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ jetzt gelöst und komme auf $u^2=3B^2x^2+\left(\alpha-\frac{6B^2}{\alpha}\right)x+\frac{6B^2}{\alpha^2}+Ce^{-\alpha x}$ mit einer frei wählbaren Konstanten C. Ich wähle $C=2A(1-2A)-\frac{6B^2}{\alpha^2}$ , wobei A eine kleine Zahl, d. h. $|A|\ll 1$ , sein soll. Weiterhin ist $\alpha x\ll 1$ , denn wir sind weit vom Schwarzschild-Radius entfernt, und es ist $B^2x^2\ll 1$ , denn der Planet ist langsam im Vergleich zum Licht. Nur unter diesen zwei Bedingungen ist Einsteins Näherung gültig. Wenn ich die Lösung nun bis zur zweiten Ordnung in $A$ , $\alpha x$ und $B^2x^2$ entwickle, komme ich auf $u^2=(2A+\alpha x)(1-2A)+\alpha B^2x^3$ .

Nun hat Einstein definiert: $s_{neu}=s\sqrt{1-2A}$ und (auch wenn er das nicht hinschreibt) $B_{neu}=B/\sqrt{1-2A}$ . $B_{neu}$ muss so definiert werden, denn sonst behält Gl. (10) nicht ihre Form. Außerdem ist $u_{neu}^2=\frac{dr^2+r^2d\phi^2}{ds_{neu}^2}$ und $u^2=\frac{dr^2+r^2d\phi^2}{ds^2}$ , woraus $u_{neu}^2=\frac{u^2}{1-2A}$ folgt. Wenn ich die letzte Gleichung für $u^2$ durch 1-2A teile, erhalte ich $u_{neu}^2=2A+\alpha x+\alpha B_{neu}^2x^3$ . Diese Lösung ist exakt bis zur zweiten Ordnung in $A$ , $\alpha x$ und $B_{neu}^2x^2$ , also eine Größenordnung genauer als die Newton-Approximation. Ich sagte schon, dass in $u^2=2A+\alpha x+\alpha B^2x^3$ das neue $u^2$ und das neue B stehen. Einstein hatte also die richtige Lösung gefunden.

In Kommentar Nr. 2074 vom 17. April 2017, 17:33 Uhr habe ich Gl. (11) ausführlich aus Gl. (7b) hergeleitet. Finden Sie darin einen Rechenfehler?

Die Gleichung $\frac{du^2}{dx}=\alpha(1+\alpha x-u^2+3B^2x^2)$ hat Engelhardt in dem Appendix seines Papers „Free Fall in Gravitational Theory“ aus Einsteins Gl. (7b) hergeleitet. Ich meine Gl. (7b) aus Einsteins Erklärung der Perihelbewegung des Merkur. Gl. (7b) hat die Konsequenz, dass $r^2\frac{d\phi}{ds}=B$ eine Konstante ist, wenn die Bewegung in der durch $\Theta=\pi/2$ definierten Ebene stattfindet. Dann gilt $\left(\frac{dx}{d\phi}\right)^2+x^2=u^2/B^2$ mit $u^2=\frac{dr^2+r^2d\phi^2}{ds^2}$ und $x=1/r$ .

Wir nehmen jetzt an, dass $u^2$ durch eine (dreifache) Reihe von Termen der Form $\gamma_{abc}A^a(\alpha x)^b(B^2x^2)^c$ gegeben ist. a,b und c sind nicht-negative ganze Zahlen. Die erste Approximative soll $u^2=2A+\alpha x$ sein, d. h. wir haben $\gamma_{000}=0$ , $\gamma_{100}=2$ , $\gamma_{010}=1$ und $\gamma_{001}=0$ . Dann hat die Lösung $x(\phi)$ die Periode $2\pi/\omega$ mit $\omega=1+\omega_2+\omega_3+\omega_4+\ldots$ . $\omega_n$ ist eine Summe von Termen (n-1)-ter Ordnung in den zwei Größen 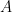$A$ und $\alpha^2/B^2$ . Man kann zeigen, dass $\omega_n$ nicht von $\gamma_{abc}$ abhängig ist, wenn $a+b+c>n$ gilt. 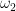Wenn wir nur $\omega_2$ berechnen wollen, brauchen wir also nur die zweite Approximative von $u^2$ berechnen, d. h. alle Terme mit $a+b+c\le 2$ .

Jetzt hat Engelhardts Differentialgleichung die exakte Lösung $u^2=3B^2x^2+\left(\alpha-\frac{6B^2}{\alpha}\right)x+\frac{6B^2}{\alpha^2}+Ce^{-\alpha x}$ mit einer frei wählbaren Konstanten C. Ich wähle $C=2A(1-2A)-\frac{6B^2}{\alpha^2}$ . Ich darf das tun, weil ich dadurch die Konstante A erstmals in die Rechnung einführe. (Die Konstante A kommt zwar schon in Einsteins Gl. (8) vor, doch Einstein hat Gl. (8) nicht bei der Herleitung von Gl. (7b) verwendet. Und wir verwenden Einsteins Gl. (8) jetzt auch nicht mehr.) Dann hat $u^2$ die im vorigen Absatz angegebene Form. Als zweite Approximative erhalten wir $u^2=(2A+\alpha x)(1-2A)+\alpha B^2x^3$ . Das setzen wir in die Gleichung $\left(\frac{dx}{d\phi}\right)^2+x^2=u^2/B^2$ ein und erhalten $\left(\frac{dx}{d\phi}\right)^2+x^2=(2A+\alpha x)(1-2A)/B^2+\alpha x^3$ . Einstein hat auf Seite 837 die Konstante B neu definiert. Auch wenn er das nicht hinschreibt, muss das neue B durch $B_{neu}=B/\sqrt{1-2A}$ gegeben sein. Und damit erhalten wir $\left(\frac{dx}{d\phi}\right)^2+x^2=(2A+\alpha x)/B_{neu}^2+\alpha x^3$ . Und das ist Einsteins Gl. (11). Wir erhalten außerdem $\omega_2=-\frac{3\alpha^2}{4B^2}=-\frac{12\pi^2a^2}{(1-\epsilon^2)c^2T^2}$ und damit Einsteins Formel für die Perihelbewegung pro Umlauf.

In erster Näherung gelten die Gleichungen $A=-\frac{2\pi^2a^2}{c^2T^2}$ und $\alpha^2/B^2=\frac{16\pi^2a^2}{(1-\epsilon^2)c^2T^2}$ . $a$ ist die große Halbachse, $\epsilon$ die Exzentrizität, $c$ die Lichtgeschwindigkeit im Vakuum und $T$ die Umlaufzeit. Für den Merkur ergibt das die Zahlenwerte $A=-1.3\cdot 10^{-8}$ und $\alpha^2/B^2=1.1\cdot 10^{-7}$ . Also wirklich sehr kleine Zahlenwerte. 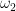Es erscheint daher gerechtfertigt, nur $\omega_2$ zu berechnen und die Berechnung von $\omega_3$ , $\omega_4$ usw. zu unterlassen.

Die Behauptung aus Engelhardts Appendix seines Papers „Free Fall in Gravitational Theory“, dass Einsteins Gl. (11) nicht aus seiner Bewegungsgleichung abgeleitet werden kann, ist also falsch.

Diesen Kommentar: Zitieren
#2630 | Martin Raible | 27. Dezember 2021, 04:42

Ich wollte „Approximation“ schreiben und nicht „Approximative“.

Diesen Kommentar: Zitieren
#2631 | Martin Raible | 27. Dezember 2021, 05:22

Ich wollte nur genauer erklären, weshalb ich die zweite Approximation berechne. Das ist der Sinn meines Beitrags.

Diesen Kommentar: Zitieren